In questo appunto di analisi matematica trattiamo delle rette asintotiche che troviamo nei grafici di funzioni reali, in particolare dell’asintoto verticale. Per determinare gli eventuali asintoti di una funzione, si devono calcolare i limiti agli estremi del suo dominio, il risultato ci fa capire se si tratta di un asintoto orizzontale, di un asintoto obliquo oppure del di un asintoto verticale. Per tale motivo è fondamentale avere familiarità con il calcolo dei limiti.
Indice
- Cosa permette di fare lo studio dei limiti di una funzione?
- Grafici di funzioni che hanno asintoti
- Definizione di asintoto per il grafico di una funzione
- Asintoto verticale per il grafico di una funzione
- Asintoto orizzontale per il grafico di una funzione
- Asintoto obliquo per il grafico di una funzione
- Analisi di alcuni grafici di una funzione con asintoti verticali e orizzontali
Cosa permette di fare lo studio dei limiti di una funzione?
La comprensione del mondo in cui viviamo dipende in gran parte dalla capacità dell’uomo di descriverne i cambiamenti. Il moto di un pallone da calcio, la traiettoria di un pianeta, le correnti marine, la temperatura degli oceani, le fluttuazioni del mercato, la diffusione di una epidemia, la crescita economica o il decadimento di una sostanza radioattiva sono tutti fenomeni che vengono normalmente studiati.In ciascuno di esse siamo inevitabilmente portati ad analizzare relazioni tra grandezze che variano nel tempo.
L’algebra e la geometria sono strumenti adeguati alla descrizione delle relazioni tra statistiche, ma non dispongono di concetti e strumenti adatti a descriverne le variazioni. A questo scopo sono necessarie operazioni matematiche diverse, che vadano oltre le operazioni algebriche, servono strumenti in grado di analizzare il modo in cui variano grandezze che sono collegate tra loro. Alla base di tutto ciò si pone l’introduzione nella matematica dei concetti di infinito, di infinitesima e di limite. Possiamo affermare che il concetto di limite costituisce la pietra di volta sulla quale si basa tutto lo sviluppo del calcolo differenziale e del calcolo integrale.
Per ulteriori approfondimenti sul calcolo integrale vedi qua
Grafici di funzioni che hanno asintoti
Curve chiuse come la circonferenza o un’ellisse nel piano cartesiano non presentano asintoti. Osservando i grafici di alcune funzioni vediamo che a volte si estendono all’infinito. I rami di una parabola o quelli dell’iperbole che sono curve aperte presentano questa caratteristica, anche la funzione esponenziale e logaritmica hanno andamenti simili. Tra le funzioni goniometriche, che sono funzioni periodiche, il grafico della tangente presenta rami che si estendono all’infinito mentre si avvicinano a rette verticali che si trovano in corrispondenza dei punti in cui la funzione non è definita.Per questi grafici possono esistere delle rette chiamate asintoti che godono della proprietà di essere tangenti alla curva all’infinito.
Il termine asintoto dal greco asymptotos, significa “che non incontra”, da cui l’aggettivo asintotico per dire che tende ad avvicinarsi sempre più a qualcosa senza mai raggiungerlo o coincidere con esso.
Definizione di asintoto per il grafico di una funzione
Utilizzando il concetto di limite e i teoremi relativi alla sua determinazione si può studiare e analizzare l’andamento di una funzione in un intorno degli estremi dell’intervalli che costituiscono il suo insieme di definizione e di individuare i suoi asintoti. Se il grafico di una funzione di equazione[math]y=f(x)[/math]
ha un ramo che si estende all’infinito, indichiamo con [math]P(x; y)[/math]
un suo generico punto; se esiste una retta [math]r[/math]
alla quale il punto P si avvicina sempre più al suo tendere all’infinito lungo quel ramo, allora la retta è chiamata asintoto del grafico.Le rette asintotiche possono essere verticali, orizzontali oppure oblique.
Nel primo caso abbiamo una retta parallela all’asse delle ordinate, nel secondo caso la retta è parallela all’asse delle ascisse, nel terzo caso si tratta di una retta con un’inclinazione qualsiasi rispetto all’asse delle ascisse, caratterizzata da un coefficiente angolare
[math]m[/math]
e un’intercetta [math]q[/math]
.Diamo una definizione generale di asintoto:
Una retta r è un asintoto per il grafico di una funzione che si estende all’infinito quando, detto P un punto del grafico e detta H la sua proiezione sulla retta, la distanza
[math]\overline{PH}[/math]
, di P da r, tende a zero quando P si sposta all’infinito, cioè al tendere all’infinito di almeno una delle coordinate di P. La conoscenza degli asintoti ci aiuta anche a tracciare il grafico probabile di una funzione.Per ulteriori approfondimenti sul grafico probabile di una funzione vedi qua
Asintoto verticale per il grafico di una funzione
Un asintoto verticale è una retta verticale del tipo di equazione generica[math]x=x_0[/math]
, i suoi punti hanno ascissa costante, si tratta di una retta parallela all'asse delle ordinate e approssima l'andamento di una funzione in corrispondenza del punto [math]x_0[/math]
.Cosa rappresenta il punto
[math]x_0[/math]
?Si tratta di un punto di accumulazione del dominio, in cui la funzione diverge, cioè tende a
[math]\pm\infty[/math]
. La funzione non è definita in questo punto ma esiste in prossimità di esso ovvero immediatamente prima e immediatamente dopo.
Detto
[math]x_0[/math]
il punto di accumulazione del dominio [math]D[/math]
della funzione [math]y=f(x)[/math]
possiamo generalizzare come segue:una retta di equazione
[math]x=x_0[/math]
è un asintoto verticale per il grafico della funzione [math]f(x)[/math]
se, per [math]x\to x_0^-[/math]
oppure [math]x\to x_0^+[/math]
, la funzione tende a [math]+\infty \ \ o \ \ -\infty[/math]
.È possibile che solo uno dei due limiti sia infinito in questo caso si parla di asintoto verticale sinistro se soltanto il limite sinistro è infinito, di asintoto verticale destro se è infinito solo il limite destro.
Asintoto orizzontale per il grafico di una funzione
Il grafico di una funzione può avere un asintoto orizzontale quando il suo dominio è illimitato ovvero gli estremi del dominio sono più e meno infinito. Bisogna calcolare i limiti in corrispondenza di questi estremi e se il risultato del limite è un numero finito reale[math]l \in \Re[/math]
allora l’equazione dell'asintoto orizzontale è: [math]y=l[/math]
.Analogamente all’asintoto verticale anche in questo caso la funzione può tendere alla retta orizzontale solo a destra oppure solo a sinistra.
Diremo perciò che la retta di equazione
[math]y=l[/math]
è un asintoto orizzontale del grafico di una funzione f(x) se:
[math]\lim_{x\rightarrow \pm \infty}{f(x)}=l[/math]
L’asintoto orizzontale è solo a destra se:
[math]\lim_{x\rightarrow +\infty}{f(x)}=l[/math]
L’asintoto orizzontale è solo a sinistra se:
[math]\lim_{x\rightarrow -\infty}{f(x)}=l[/math]
Precisiamo che il grafico di una funzione può avere contemporaneamente un asintoto orizzontale destro e sinistro distinti tra loro, in questo caso i due limiti saranno distinti:
[math]\lim_{x\rightarrow +\infty}{f(x)}=l_1\ \ e \ \ lim_{x\rightarrow -\infty}{f(x)}=l_2 \wedge l_1\neq l_2 [/math]
Osservazione
Per avere degli asintoti orizzontali è necessario che il dominio della funzione sia illimitato e la funzione non sia periodica.
Se il dominio è un intervallo chiuso e limitato sicuramente non ammette asintoti orizzontali. Vedi ad esempio il grafico delle funzioni seno e coseno, funzioni oscillanti ma prive di asintoti perché il loro codominio è limitato.
La funzione arcotangente, inversa della tangente, è definita in
[math]\Re[/math]
ed ha due asintoti orizzontali: [math]y= \pm {\pi\over 2}[/math]
Per ulteriori approfondimenti sugli asintoti vedi quaPer ulteriori approfondimenti sulle funzioni goniometriche inverse vedi qua
Asintoto obliquo per il grafico di una funzione
Se calcolando i limiti agli estremi del dominio illimitato, il risultato è ancora più o meno infinito, non ci sono asintoti orizzontali ma è possibile che la funzione tenda, in maniera asintotica, ad una retta obliqua di generica equazione:
[math]y=mx+q[/math]
Questa retta è un asintoto obliquo per il grafico della funzione se:
[math]\lim_{x\rightarrow \pm \infty}{[f(x)-(mx+q)]}=0[/math]
I due parametri m e q, rispettivamente coefficiente angolare e ordinata all’origine della retta, si calcolano mediante i seguenti limiti:
[math]m=\lim_{x\rightarrow \pm \infty}{\frac {f(x)}{x}}[/math]
[math]q=\lim_{x\rightarrow \pm \infty}{[f(x)-mx]}[/math]
Anche in questo caso Si può verificare che la condizione sia soddisfatta o solo per x che tende a più infinito e in questo caso si ha l’asintoto obliquo destro oppure solo per x che tende a meno infinito e pertanto si ha asintoto obliquo sinistro.
Riepilogando
- Gli eventuali asintoti per il grafico di una funzione devono essere ricercati agli estremi del dominio [math]D[/math]della funzione
- Agli estremi finiti del dominio che non appartengono a D potrebbero esistere asintoti verticali
- Agli estremi infiniti del dominio potrebbero esistere asintoti orizzontali oppure asintoti obliqui
Analisi di alcuni grafici di una funzione con asintoti verticali e orizzontali
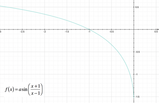
Vediamo ora un processo a ritroso ovvero a partire dal grafico di una funzione cerchiamo di capire se questa presenta degli asintoti e di che natura essi sono.Nella figura sottostante ci sono due funzioni (a) e (b).
La funzione (a) è definita per ogni valore reale tranne che nel punto -1.
In corrispondenza di questo valore la retta verticale tratteggiata rappresenta l’asintoto verticale della funzione e si tratta di un asintoto verticale sia sinistra che a destra. I due rami del grafico salgo sempre più in alto avvicinandosi a questa retta da entrambi i lati.
La funzione presenta anche due asintoti orizzontali uno è l’asse delle ascisse solo a sinistra dove il ramo vi si avvicina quando la x tende a meno infinito. L’altro ramo della funzione tende all’asintoto orizzontale di equazione
[math]y=-2[/math]
e questo è un asintoto orizzontale solo a destra che si ottiene per x che tende a più infinito.Nel grafico (b) il punto di accumulazione è
[math]x=0[/math]
, riconosciamo come asintoto verticale ancora uno degli assi cartesiani quello delle ascisse e la retta di equazione [math]y=1[/math]
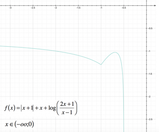
. Notiamo inoltre che in questo caso vi è anche un’intersezione tra la funzione e l’asintoto orizzontale. Analizziamo ancora un altro grafico.
La funzione rappresentata non è definita in
[math]]0; 2[[/math]
e nel punto 7. Il dominio presenta tre punti di accumulazione in cui abbiamo 3 asintoti verticali.La funzione presenta anche due asintoti orizzontali uno di equazione
[math]y=2[/math]
solo a sinistra, quando x tende a meno infinito, l’altro è l’asse delle ascisse [math]y=0[/math]
solo a destra, quando la x tende a più infinito.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
