Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

di _stan

Ominide

4 min. di lettura

Vota

La funzione in questione è una funzione trigonometrica, e in particolare è la funzione inversa della funzione seno. In questo caso, sapendo che il seno di un angolo è sempre un valore compreso tra -1 e 1, possiamo imporre che:

[math] -1 >= frac(x+1)(x-1) >= 1 [/math]

Per poter risolvere questa disequaizone dobbiamo imporre un sistema:

[math] \begin{cases} frac(x+1)(x-1) >= 1 \\ frac(x+1)(x-1) >= -1 \ \end{cases} [/math]

Ovvero:

[math]\begin{cases} frac(x+1 - x + 1)(x-1) >= 0 \\ frac(x+1+ x - 1 )(x-1) >= 0 \ \end{cases}[/math]

[math]\begin{cases} frac(2)(x-1) >= 0 \\ frac(2x)(x-1) >= 0 \ \end{cases}[/math]

Risolvendo le due disequazioni si ottiene il seguente sistema:

[math] \begin{cases} x >=1 \\ x >= 0 V x > 1 \ \end{cases} [/math]

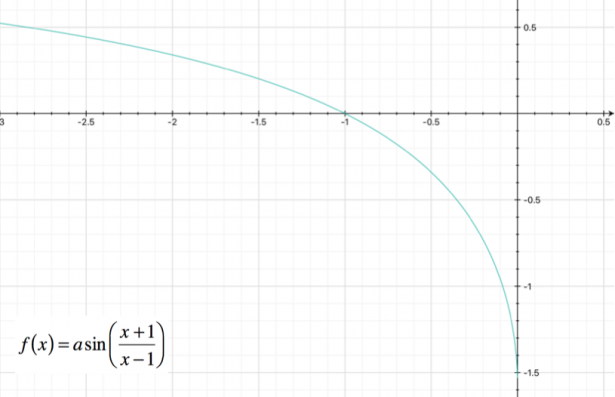
Le soluzioni del sistema sono rappresentate dal seguente intervallo

[math] ( -oo ; 0 ] [/math]

, che rappresenta il dominio della funzione.

Determiniamo ora i punti di intersezione con gli assi:

[math] f(x) _|_ (x = 0) [/math]

[math] f(0) = arc\\sin (frac(0+1)(0-1)) = arc\\sin(-1) = - π/2 [/math]

Il punto individuato è

[math] ( 0 ; -π/2 ) [/math]

[math] f(x) _|_ (y = 0) [/math]

[math] f(x) = 0 \to arc\\sin (frac(x+1)(x-1)) = 0 [/math]

[math] frac(x+1)(x-1) = 0 \to x + 1 = 0 \to x = - 1 [/math]

Otteniamo il punto

[math] ( -1 ; 0 ) [/math]

Verifichiamo se la funzione è pari o dispari:

[math] f(-x) = arc\\sin (frac(-x+1)(-x-1)) [/math]

La funzione quindi non è ne pari ne dispari.

Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso il limite a

[math]-oo[/math]

[math] lim_(x \to -oo) arc\\sin (frac(x+1)(x-1)) [/math]

Non vi sono in questo limite forme di indecisione, in quanto la frazione che è argomento del'arcoseno presenta numeratore e denominatore dello stesso grado; si ha quindi:

[math] lim_(x \to -oo) arc\\sin (frac(x+1)(x-1)) = arc\\sin(1) = π/2 [/math]

Ha come asintoto orizzontale la retta di equazione

[math] y = π/2[/math]

Studiamo ora il comportamento della derivata prima della funzione:

[math] f'(x) = frac(1)(\sqrt{1 - (frac(x+1)(x-1))^2} ) = frac(1)(\sqrt(1 - frac((x+1)^2)((x-1)^2)) ) = [/math]

[math] frac(1)(\sqrt{frac( (x-1)^2 - (x+1)^2)((x-1)^2)} ) = frac( | x - 1| )(\sqrt( (x-1)^2 - (x+1)^2) ) =[/math]

[math] frac( | x - 1| )(\sqrt{ x^2 + 1 - 2x - x^2 - 1 - 2x} ) = frac( | x - 1| )(\sqrt(- 4x) ) [/math]

Poiché la funzione è definita per

[math]x > 0[/math]

, e sapendo che

[math]| x - 1| = x - 1 se x >= 1 [/math]

[math]| x - 1| = - x + 1 se x > 1[/math]

Possiamo scrivere la derivata prima in questo modo:

[math] f'(x) = frac( 1 - x )(\sqrt{- 4x} ) [/math]

Troviamo i punti in cui la deriva prima si annulla:

[math] f'(x) = 0 \to frac( 1 - x )(\sqrt{- 4x} ) = 0 [/math]

[math] 1 - x = 0 \to x = 1 [/math]

Tale punto, però, non appartiene al dominio della funzione; studiamo il segno della derivata prima:

[math] f'(x) > 0 \to frac( 1 - x )(\sqrt{- 4x} ) > 0 [/math]

[math] 1 - x > 0 [/math]

[math] \sqrt{- 4x} > 0 [/math]

Dallo studio del segno si ottengono i seguenti intervallo:

[math] ( 0; +oo ) [/math]

; tale intervallo non appartiene al dominio della funzione e quindi, poiché la derivata prima è negativa nei punti del dominio, sappiamo che la funzione sarà decrescente in tutto il dominio.

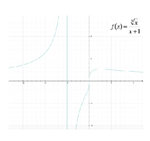
Possiamo procedere rappresentando il grafico approssimativo della funzione:

Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

La funzione in questione è una funzione trigonometrica, e in particolare è la funzione inversa della funzione seno. In questo caso, sapendo che il seno di un angolo è sempre un valore compreso tr...

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Appunti correlati

Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.