Tavola pitagorica, origini e curiosità

In questo appunto di matematica ripercorriamo le origini della tavola pitagorica, strumento di calcolo rapido, noto a tutti noi, fin dalle scuole elementari Per effettuare moltiplicazioni e divisioni tra numeri interi. L’attribuzione al filosofo Pitagora o a qualche suo discepolo, è probabilmente il risultato di un errore di trascrizione, ciò poco importa perché questo strumento per quanto semplice ma geniale segna il passaggio dal rudimentale abaco antico romano, con scanalature sassolini e gettoni, al sistema posizionale decimale che utilizza solo cifre.

Moltiplicazione in

[math]N[/math]

, definizione e proprietà

Nell’insieme dei numeri naturali la moltiplicazione è un’operazione interna che a qualsiasi coppia di numeri naturali

• Commutativa, qualunque siano i numeri naturali a e b si ha che:
  [math]a×b=b×a[/math]
• Associativa, qualunque siano i numeri naturali a, b e c si ha che:
  [math]a×(b×c)=(a×b)×c=a×b×c[/math]
• Distributiva rispetto all’addizione, qualunque siano i numeri naturali a, b e c si ha che:
  [math]a×(b+c)=(a×b)+(a×c)[/math]
• Esistenza dell’elemento neutro, qualunque sia il numero naturale a si ha che:
  [math]a×1=1×a=a[/math]
• Esistenza dell’elemento nullo o assorbente, qualunque sia il numero naturale a si ha che:
  [math]a×0=0×a=0[/math]
• Compatibilità con la relazione di ordine in N, qualunque siano i numeri naturali a, b e c, se a<b si ha che:
  [math]a×c<b×c[/math]

Le tecniche per svolgere le moltiplicazioni presuppongono:

• la conoscenza della tavola pitagorica
• la scomposizione di un numero in unità decine centinaia,….
• la conoscenza della proprietà associativa
• la conoscenza della proprietà distributiva

Per ulteriori approfondimenti sulla moltiplicazione vedi qua

Uso dell'abaco

L'abaco consiste in una serie di aste verticali infilate in un sostegno di base, ogni asta rappresenta un ordine di grandezza il cui valore è dato dalla posizione che occupa.

Sull'abaco in base 10 su ogni asta ci stanno 9 palline: quindi se ho 10 unità di un certo ordine le cambio con una sola pallina dell'asta successiva.
Lo zero è rappresentato da un'asta priva di palline. A differenza dei blocchi aritmetici multibase, l'abaco è uno strumento più astratto perché uno stesso simbolo,la pallina, cambia valore a seconda della posizione che occupa l'asta in cui viene collocata punto l'uso di entrambi questi materiali, abaco e blocchi, consente però di:

• padroneggiare il sistema di cambio da un ordine di grandezza a un altro;
• comprendere il valore posizionale delle cifre;
• comprendere il sistema convenzionale di scrittura dei numeri;
• eseguire equivalenze fra unità, decine, centinaia;
• eseguire riporti e prestiti nei calcoli.

Per ulteriori approfondimenti sui sistemi di numerazione in base qualsiasi vedi qua

Tavola pitagorica: cos’è

Molto comoda per moltiplicazioni e divisioni è stata la Tavola Pitagorica, su cui tutti gli studenti delle elementari hanno studiato le cosiddette “tabelline”. In origine il quadrato era composto da 100 caselle, 10 per lato: sulla prima fila in orizzontale e verticale ci sono i multipli di uno, sulla seconda i multipli di 2 e così via.
Ogni riga e ogni colonna costituiscono una progressione aritmetica la cui ragione è uguale al numero posto nella prima casella. I numeri posti sulla diagonale principale (da sinistra in alto a destra in basso) sono il quadrato dei primi 10 numeri naturali. I numeri sulla diagonale secondaria (da destra in alto a sinistra in basso) sono composti di due fattori, di cui il primo aumenta di una unità e il secondo diminuisce, ad esempio:

• 10=1x10
• 18=2x9
• 24=3x8

Per effettuare una operazione di moltiplicazione tra due numeri naturali posti sui due lati, nel punto di incontro si troverà il risultato. Vogliamo eseguire il prodotto tra gli interi 8 e 9. Osserviamo la figura della tavola riportata in basso: dobbiamo partire dalla colonna blu con il numero 8 e muoverci in orizzontale fino ad incontrare la colonna che scende dal 9 che si trova sulla riga blu in alto. Il risultato del prodotto tra questi due numeri lo leggiamo nella casella di incrocio:

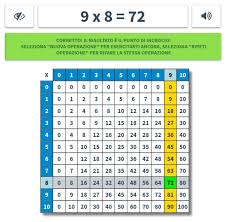
Sempre utilizzando la tavola pitagorica è possibile anche effettuare una divisione tra un numero posto all’interno e uno dei due numeri adesso corrispondente sui lati, il risultato della divisione comparirà nel lato opposto. Nell’esempio riportato in basso è stata effettuata la divisione tra il numero 20 e il numero 5. Il risultato di questa divisione lo leggiamo muovendoci a sinistra del numero 20 fino ad incontrare la casella evidenziata cioè 4 nella prima colonna, come indicano le frecce.

Per ulteriori approfondimenti sulle progressioni vedi qua

Tavola pitagorica: storia

(filosofo vissuto nel 500 dopo Cristo), nel libro "Geometria" scrive che i discepoli di Pitagora, per non fare errori di calcolo nella moltiplicazione e nella divisione si servivano di una figura particolare alla quale diedero il nome di tavola o mensa pitagorica in onore del loro maestro. Il libro di Severino Boezio nel Medioevo era molto conosciuto particolarmente per opera del papa Silvestro II (morto nel 1003) che diffuse in Europa il calcolo in base 10. Boezio è stato un illustre uomo di cultura del suo tempo e con la diffusione dei suoi scritti ha contribuito alla trasmissione della cultura classica soprattutto. Conoscenze di: aritmetica, geometria, musica e filosofia sono state tramandare e diffuse grazie alle sue opere. Fu imprigionato a Pavia e poi decapitato nel 524, con l’accusa di tradimento al potere ostrogoto; durante l’età medievale è stato considerato un vero e proprio martire degli intrighi politici.
La tavola pitagorica riportata da Boezio si ferma alla colonna del 9.
Per approfondimenti su Severino Boezio vedi qua

Tavola pitagorica: un falso storico

Nel paragrafo precedente abbiamo letto il motivo per cui si parla di Tavola Pitagorica. In realtà un errore di trascrizione dovuto ad un copista dell'opera Ars Geometrica di Boezio sostituì l'abaco neopitagorico con la comune tavola di moltiplicazione, di aspetto assai simile, conservando però per quest'ultima il nome di Tavola Pitagorica, che invece designava l'abaco neopitagorico. Dunque, la tavola di moltiplicazione che tutti noi conosciamo come Tavola Pitagorica non deve il suo nome né a Pitagora né ad alcun suo seguace, bensì soltanto a un errore ditrascrizione.
Tutti i popoli dell’antichità hanno costruito strumenti per effettuare il calcolo strumentale. Al giorno d’oggi tutti abbiamo una calcolatrice che usiamo quotidianamente per effettuare rapidamente 4 operazioni aritmetiche.
L’abaco utilizzato dai romani e anche da Fenici, Ebrei, Greci ed Etruschi si chiamava abaco a polvere: era una tavoletta rettangolare fatta di legno o di bronzo sulla quale era incollata della polvere di colore verde. Adoperando una bacchetta si potevano tracciare simboli numerici e figure geometriche, in pratica era una primitiva lavagna.
I babilonesi utilizzavano uno strumento fatto di marmo sempre di forma rettangolare sul quale erano incisi due gruppi di 11 linee verticali attraversate da una linea orizzontale.
Sempre i romani adottarono altri due tipi di abaco: quello a lapilli e quello a bottoni.
La versione medievale a colonne o a gettoni dell’abaco romano risultò uno strumento di calcolo in perfetta sintonia con il sistema di numerazione posizionale in forma critta.