Circonferenza: definizione, equazione e risoluzione di problemi

In questo appunto di Geometria verrà prima introdotta la definizione di Circonferenza con relativa equazione per la rappresentazione nel piano cartesiano, per poi essere utilizzata nella risoluzione di problemi di geometria analitica.

Definizione ed equazione della Circonferenza

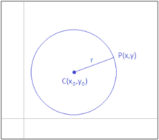
Si definisce Circonferenza il luogo geometrico dei punti del piano cartesiano equidistanti da un punto fisso detto centro; mentre, la distanza di qualsiasi punto della circonferenza dal centro si definisce raggio della circonferenza.

Di conseguenza i punti di coordinate (x,y) appartenenti alla circonferenza di raggio r e centro O di coordinate

, devono soddisfare la seguente equazione:

Quest’equazione può anche essere scritta nella sua forma canonica, ovvero:

Dove:

;

;

Se il centro della circonferenza coincide con l’origine, cioè O(0,0), allora avremo che:

e

Di conseguenza, l’equazione della circonferenza si riduce a:

Quella appena ricavata è quindi l’equazione della circonferenza con centro sull’origine degli assi cartesiani.
A questo punto, è lecito chiedersi se, data un’equazione qualunque, com’è possibile riconoscere se si tratta dell’equazione di una circonferenza o meno?
Per rispondere a questa domanda basta porre maggiore attenzione sulla forma dell’equazione della circonferenza; in particolare, abbiamo che:

• Intanto si tratta di un’equazione di II grado in due incognite, ovvero x ed y.
• i coefficienti dei termini di secondo grado della x e della y devono essere uguali;
• nell’equazione non è presente il termine misto xy;
• il valore del raggio deve essere sempre positivo, ergo non esiste una circonferenza con raggio negativo; la distanza tra un qualunque punto della circonferenza e il centro è sempre positiva. Inoltre, se riguardiamo la formula di r, vediamo che essa è definita a partire dalla radice quadrata e la radice quadrata di un numero razionale non è mai negativa.

Dopo questa breve introduzione possiamo passare al prossimo paragrafo dove sono presenti alcune applicazioni/riflessioni di quanto detto finora.

Applicazione dell’equazione della circonferenza

In questo paragrafo vedremo alcuni esercizi di geometria analitica in cui è applicheremo quanto detto nel paragrafo precedente. In realtà si tratta di ragionamenti ed osservazioni che ci permettono di comprendere meglio l’equazione della circonferenza. Vediamone alcuni:
Com’è possibile verificare se un punto P, di coordinate

Di conseguenza, possiamo avere tre casi:

• se tale distanza è minore del raggio (
  [math]d>r[/math]
  ) allora il punto è interno al cerchio;
• se la distanza è maggiore del raggio (
  [math]d>r[/math]
  ) allora il punto è esterno al cerchio;
• Infine se tale somma è uguale al raggio (
  [math]d=r[/math]
  ), allora il punto appartiene alla circonferenza.

Data una circonferenza, come si trovano i punti d'incontro, cioè i punti in comune, tra una circonferenza ed una retta?
In questo caso basta risolvere il sistema di equazioni composto dall’equazione della circonferenza e quella della retta. Ovviamente, in base al numero di soluzioni possiamo dire che la retta è:

• tangente alla circonferenza se hanno un solo punto in comune;
• secante alla circonferenza se hanno due punti in comune;
• esterna alla circonferenza se non hanno alcun punto in comune.

Lo stesso discorso può essere fatto anche per il caso di due circonferenze, o una circonferenza e un all’ellisse, o qualunque altra figura geometrica/funzione espressa all’interno del piano cartesiano.
Com’è possibile verificare che una retta è esterna, tangente o secante ad una circonferenza?
In questo caso ci sono due procedimenti possibili:

• In maniera analoga al caso del punto P, anche nel caso della retta bisogna fare riferimento alla distanza. In particolare, si calcola la distanza dal centro della circonferenza O(x,y) alla retta: se tale distanza è maggiore del raggio allora la retta è esterna, se è uguale al raggio allora la retta è tangente, infine se tale distanza è minore del raggio allora la retta è secante alla circonferenza;
• Si può risolve il sistema dato dall'equazione della circonferenza e l'equazione della retta. In questo caso si ottiene un’equazione di secondo grado della quale possiamo calcolare il discriminante
  [math]\Delta[/math]
  : se
  [math]\Delta>0 [/math]
  allora la retta è esterna (nessuna intersezione), se
  [math]\Delta=0 [/math]
  allora la retta è tangente (abbiamo due punti coincidenti), mentre se
  [math]\Delta>0 [/math]
  allora la retta è secante (due punti distinti, cioè due intersezioni).

Nel prossimo paragrafo vedremo qualche applicazione di quanto detto per la risoluzione di alcuni esercizi.

Esercizi sulla circonferenza

Dopo aver compreso meglio l’equazione della circonferenza e le possibili relazioni con punti, rette e circonferenze che, come abbiamo detto, possono essere interne, esterne o tangenti alla circonferenza, passiamo adesso alla risoluzione di alcuni esercizi.

• Scrivere l'equazione della retta uscente da un punto e tangente ad una circonferenza:
Premettiamo il fatto che se il punto in questione è esterno ad una circonferenza, allora ci sono due rette tangenti alla circonferenza. Al contrario, se il punto appartiene alla circonferenza allora vi è una sola retta tangente; infine, se il punto è interno alla circonferenza allora da esso non possono essere tracciate rette tangenti alla circonferenza.
Detto questo, possiamo procedere con la risoluzione del sistema dato dall'equazione della circonferenza e il fascio proprio di rette uscenti dal punto. La soluzione di questo sistema sarà un'equazione parametrica di secondo grado nel parametro m. Dopodiché, imponendo
[math]\delta=0[/math]
si possono trovare 2 valori di m se il punto è esterno, un solo valore di m se il punto appartiene alla circonferenza. Sostituendo questi valori di m nel fascio di rette, si trovano infine le tangenti alla circonferenza.

• Scrivere l'equazione di una circonferenza della quale vengono date le coordinate dei 2 punti estremi del diametro
In generale, per scrivere l’equazione di una circonferenza è necessario conoscere le coordinare del centro e la misura del raggio. In questo caso ci viene fornito il diametro in quanto corrisponde alla distanza tra i due punti in questione, di conseguenza possiamo calcolare il raggio dividendo il diametro per 2. Dopodiché basta pensare al fatto che il centro della circonferenza coincide con il punto medio del diametro, quindi possiamo calcolare le coordinate del punto medio tra i 2 punti dati. Mentre la semidistanza tra i due punti dati risulta essere il raggio. A questo punto, calcolate le coordinate del centro e della semi distanza, si può passare al calcolo dell'equazione della circonferenza.

• Scrivere l'equazione della circonferenza che passa per 3 punti (A,B e C) dei quali vengono date le coordinate

Si può procedere in questo modo: per prima cosa si scrivono le equazioni delle rette passanti per due punti, rispettivamente per i punti A e B, e per i punti B e C; si risolve il sistema tra questi 2 assi e si trova il centro della circonferenza; si calcola quindi la distanza tra centro e un punto qualunque della circonferenza, cosi da ottenere il raggio; infine, noti centro e raggio infine si scrive l'equazione della circonferenza.