Angoli alla circonferenza: definizione e dimostrazione di teoremi

In quest'appunto troverai una definizione generale di angolo alla circonferenza, con annessa dimostrazione di un teorema fondamentale.

La circonferenza e il cerchio: formule e differenze

La geometria piana è la branca della matematica che studia le figure piane, ossia le figure aventi due dimensioni: larghezza e altezza.
Esse possono essere caratterizzate attraverso il calcolo di due grandezze cioè il perimetro e l'area.

Il perimetro non è altro che la somma della lunghezza dei segmenti che compongono il bordo della figura mentre l'area è l'estensione della parte di piano racchiusa nel perimetro.

Esistono delle figure piane in cui il contorno non è definito da una linea spezzata chiusa, cioè da una successione di segmenti consecutivi aventi direzioni differenti (così come accade, ad esempio, per il quadrato, il triangolo etc.). In questo caso, le figure piane vengono definite non poligonali; un chiaro esempio di figura piana non poligonale è il cerchio.

Prima di parlare del cerchio è necessario stabilire la differenza tra questo termine e il termine circonferenza. La circonferenza è infatti l'insieme dei punti equidistanti (cioè posti a distanza fissata) rispetto a un punto specifico chiamato centro: la distanza fissata prende il nome di raggio.
In altre parole, il termine cerchio fa riferimento all'intera figura (ossia circonferenza più area inclusa) mentre la circonferenza descrive unicamente il contorno del cerchio.

Cos'è un angolo alla circonferenza e un angolo al centro come si definiscono

Prima di presentare la formula per il calcolo dell'area e del perimetro di un cerchio è necessario fare un elenco dei principali elementi di tale figura. Essi sono:

• il raggio, cioè la distanza tra i punti della circonferenza e il centro del cerchio
• la corda, ossia i segmenti che uniscono due punti della circonferenza. Il diametro può essere considerata la corda di massima lunghezza poiché non è altro che una corda passante per il centro
• il diametro, cioè il doppio del raggio
• l'angolo al centro, cioè un angolo avente vertice nel centro della circonferenza. I punti di intersezione tra le semirette dell'angolo e la circonferenza stessa definiscono un arco.
• l'angolo alla circonferenza, ossia un angolo cui vertice giace in un punto della circonferenza. Anche in questo caso, prolungando le semirette dell'angolo in direzione della circonferenza, è possibile tracciare un arco definito arco corrispondente all'angolo

.

A partire da questi concetti si definiscono delle formule utili al calcolo del perimetro e dell'area. In particolare, il perimetro (ossia la lunghezza della circonferenza) è calcolabile come

mentre l'area come

. In entrambe le formule, la lettera

allude al raggio.
Anche i teoremi possono avere un ruolo importante nella risoluzione degli esercizi, poiché permettono di semplificare e velocizzare il calcolo mediante delle assunzioni. Nei prossimi paragrafi, verrà dimostrato un teorema che mette in relazione l'ampiezza di un angolo al centro e dell'angolo alla circonferenza corrispondente.

I teoremi sugli angoli alla circonferenza: dimostrazione

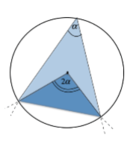
Enunciato: Dato un angolo che ha un vertice sulla circonferenza (chiamato angolo alla circonferenza), definiamo angolo al centro l'angolo che ha vertice nel centro della circonferenza e insiste sullo stesso arco in cui insiste l'angolo alla circonferenza.

Proviamo a dimostrare che l'angolo al centro è il doppio dell'angolo alla circonferenza.

Dimostrazione del teorema degli angoli alla circonferenza

Considero una circonferenza

di centro

. Sia

l'angolo alla circonferenza e sia

l'angolo al centro.

La prima osservazione che facciamo è che, per il teorema diretto del triangolo isoscele, i triangoli

e

sono isosceli. Essi possiedono infatti due lati congruenti, rispettivamente

e

. Essi sono congruenti perché sono tutti raggi della circonferenza

.

Allora gli angoli

e

sono congruenti, cioè

. Tale discorso può essere anche esteso agli angoli

e

, per cui

.

Ora prolunghiamo il segmento

dalla parte di

di un segmento

tale che OH interseca

in

.
Consideriamo il triangolo

: l'angolo

è l'angolo esterno di

. Per il Secondo Teorema dell'angolo esterno abbiamo che per gli angoli

vale che:

. Sarebbe la stessa cosa dire, siccome sono angoli congruenti, che

.
Allo stesso modo,

è l'angolo esterno di

. Allora

.

La tesi è che

.

.
In questo caso, con il secondo teorema dell'angolo esterno abbiamo dimostrato che:

.
Raccogliendo a fattor comune si ha che

. Così facendo, si ottiene la tesi.

Per ulteriori approfondimenti sugli angoli alla circonferenza vedi anche qui