Lati congruenti e poligoni

In questo appunto di matematica si trattano le varie figure geometriche aventi la caratteristica di avere alcuni o tutti i lati congruenti e le proprietà che ne derivano.

Lati congruenti

I lati di una qualunque figura geometrica sono i segmenti che delimitano la porzione di piano la quale identifica la figura geometrica in questione.
Due o più segmenti (e quindi lati) si definiscono geometricamente congruenti se tramite un movimento rigido (definito come concetto primitivo) è possibile far coincidere i due estremi dei segmenti: questo significa che, dati due segmenti di cui il primo di estremi e ed il secondo di estremi e , a movimento compiuto, l’estremo del primo segmento coincide con l’estremo del secondo segmento e l’estremo del primo segmento coincide con l’estremo del secondo segmento.
I punti del primo segmento si dicono corrispondenti od omologhi rispettivamente dei punti e del secondo segmento.
La congruenza fra segmenti gode delle tre seguenti proprietà:

• proprietà riflessiva dell’uguaglianza;
• proprietà simmetrica dell’uguaglianza;
• proprietà transitiva dell’uguaglianza.

La proprietà riflessiva asserisce che ogni segmento è uguale a se stesso.
La proprietà simmetrica prova che se un segmento è uguale ad un secondo segmento , allora anche il segmento è uguale al primo segmento :

se

allora

La proprietà transitiva afferma che se un primo segmento

è uguale ad un secondo segmento e questo a sua volta è uguale ad un terzo segmento , allora anche il primo segmento è uguale al terzo :
se

e

allora

Tali proprietà possono essere estese dai segmenti a tutte le figure geometriche.
La congruenza dei lati di una figura geometrica implica alcune importanti proprietà della stessa figura che di seguito descriviamo, suddividendo le figure geometriche in categorie distinte caratterizzate dal numero di lati.

Triangoli

I triangoli che hanno alcuni o tutti i lati congruenti sono due:

• triangolo isoscele;
• triangolo rettangolo isoscele;
• triangolo equilatero.

Il triangolo isoscele generico ha due lati uguali, questo implica che l’altezza relativa al terzo lato, la base, suddivide il triangolo di partenza in due triangoli rettangoli uguali per il secondo criterio di congruenza. Ne deriva che un triangolo isoscele, oltre ad avere due lati congruenti, ha anche gli angoli alla base uguali e l’altezza relativa alla base è anche mediana della base e bisettrice dell’angolo al vertice.
Il triangolo rettangolo isoscele, è un triangolo rettangolo con i cateti congruenti e gode di tutte le proprietà sopra elencate per i triangoli isosceli generici. La base è costituita dall’ipotenusa e l’altezza ad essa relativa suddivide il triangolo rettangolo isoscele di partenza in altri due triangoli rettangoli isosceli aventi per ipotenusa i cateti del triangolo rettangolo di partenza.
Il triangolo equilatero gode della proprietà di avere tutti e tre i lati congruenti, questo comporta che siano congruenti anche i tre angoli (pari ciascuno a 60°), per cui un triangolo equilatero viene anche detto equiangolo.
L’uguaglianza dei lati e conseguentemente degli angoli implica l’uguaglianza delle tre altezze e delle tre mediane (relative a ciascun lato) e delle tre bisettrici (relative a ciascun angolo).
Ciascuna altezza (o mediana o bisettrice) suddivide il triangolo di partenza in due triangoli rettangoli uguali aventi angoli acuti di 30° e 60°.
Per tali triangoli valgono le seguenti relazioni:
siano
h una delle altezze
l uno dei tre lati
si ha che

ossia

Inoltre si ha che l’area può essere ottenuta come:

Per quanto riguarda i triangoli, inoltre, la congruenza dei lati implica il Terzo Criterio di Uguaglianza, ossia:
due triangoli che hanno i lati rispettivamente uguali, sono uguali.
Tali triangoli possono essere di qualsiasi tipo (scaleno, isoscele, rettangolo, equilatero), l’uguaglianza fra i lati garantisce l’uguaglianza dei triangoli e conseguentemente anche l’uguaglianza fra gli angoli.

Quadrilateri

I quadrilateri aventi i lati congruenti possono essere raggruppati in diverse categorie. In questo appunto affronteremo quelli che sono di maggiore interesse a livello scolatisco.
I quadrilateri possono avere:

• due lati congruenti (singolarmente o a due a due);
• tre lati uguali;
• quattro lati uguali.

I quadrilateri con due lati congruenti di maggiore interesse sono il trapezio isoscele (solo due lati uguali) e tutti i parallelogrammi (lati paralleli a due a due) che includono ovviamente anche rombi, rettangoli e quadrati.
Il trapezio isoscele, come è noto, è un quadrilatero avente due lati paralleli e due lati obliqui uguali.
Inoltre si può avere il trapezio rettangolo con una delle due basi congruente all’altezza.
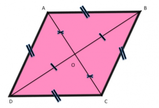
La categoria dei parallelogrammi include tutti quei quadrilateri aventi i lati opposti congruenti.
Questa caratteristica implica che anche gli angoli siano a due a due uguali: per dimostrarlo basta verificare, tramite il terzo principio di congruenza dei triangoli, che i triangoli ottenuti tracciando una diagonale del quadrilatero sono uguali.
Se sono uguali a due a due anche gli angoli, i lati opposti del parallelogramma sono paralleli a due a due.
In ogni parallelogramma:

• ciascuna diagonale lo divide in due triangoli uguali;
• i lati opposti sono uguali;
• gli angoli opposti sono uguali;
• gli angoli adiacenti a ciascun lato sono supplementari.

Le caratteristiche sopra elencate possono essere definite come i criteri principali per riconoscere se un quadrangolo convesso è un parallelogramma.
Nella categoria dei parallelogrammi rientrano molti quadrilateri.
Il rettangolo è un parallelogramma avente tutti gli angoli retti, per cui le diagonali, oltre a dividersi ciascuna a metà, sono uguali fra loro.
Il quadrilatero con tre lati uguali è il trapezio isoscele avente la base minore uguale ai lati obliqui.
La categoria dei quadrilateri con quattro lati congruenti è costituita da rombi e quadrati.
Il rombo è un parallelogramma avente quattro lati uguali (ma angoli uguali a due a due), conseguentemente le sue diagonali (di lunghezza diversa come in tutti i parallelogrammi generici) sono fra loro perpendicolari.
Il quadrato è un parallelogramma avente tutti i lati uguali e tutti gli angoli uguali, oppure, analogamente potrebbe essere definito un rettangolo con tutti i lati uguali, oppure un rombo con gli angoli retti.
In generale potremmo dire che, dato l’insieme dei parallelogrammi, rombi, quadrati e rettangoli costituiscono dei sottoinsiemi: un rombo, un quadrato ed un rettangolo per essere tali devono essere necessariamente parallelogrammi.
Si noti che, a differenza dei triangoli, la congruenza fra i lati di due o più quadrilateri non implica la congruenza delle figure geometriche. Si pensi ad esempio ad un rombo che ha i lati congruenti a quelli di un quadrato: pur avendo i lati uguali le due figure non possono essere definite geometricamente congruenti, poiché eseguendo un movimento rigido non possono essere portate a coincidere (causa la diversità degli angoli).

Poligoni

Un poligono convesso di n lati è la figura geometrica che si ottiene dall’intersezione di un dato numero n di semipiani delimitato da una poligonale chiusa A, B, C, D,… tale che considerati due suoi qualunque vertici consecutivi, ad esempio A e B, tutti i restanti vertici appartengono ad uno solo dei due semipiani di origine AB.
Un qualunque poligono convesso avente tutti i lati e gli angoli uguali viene definito regolare.
Un poligono avente i lati congruenti, ma gli angoli diversi non può essere definito regolare. Inoltre la congruenza fra più poligoni richiede l’uguaglianza di tutti gli angoli oltre che di tutti i lati.

per ulteriori approfondimenti sui poligoni con lati congruenti vedi anche qua