Dimostra che se un parallelogramma ha quattro lati congruenti allora le diagonali sono perpendicolari.
Risoluzione
Sappiamo che in ogni parallelogramma le diagonali si tagliano a metà; possiamo allora affermare che:
[math] \bar{AO} â
\bar{OC} [/math]
[math] \bar{DO} â
\bar{OB} [/math]
Inoltre, sappiamo per ipotesi che:
[math] \bar{AB} â
\bar{BC} â
\bar{CD} â
\bar{DA} [/math]
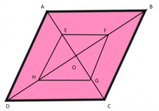
Consideriamo ora i quattro triangoli che si formano dalle diagonali:
[math]ABO[/math]
, [math]BOC[/math]
, [math]COD[/math]
, [math]DOA[/math]
.Ciascuno di essi ha un lato che è il lato del parallelogramma, e due lati in comune con altri due triangoli, cosicché tutti hanno tre lati congruenti agli altri tre triangoli.
Quindi, per il terzo criterio di congruenza dei triangoli, essi sono tutti e quattro congruenti. Possiamo quindi affermare che gli angoli
[math]Ahat OB[/math]
, [math]Bhat OC[/math]
, [math]Chat OD[/math]
, [math]Dhat OA[/math]
.sono congruenti.
Poiché essi sono angoli che formano un angolo giro (360°), e sono quattro, ciascuno di essi misurerà 90°.
Le diagonali del parallelogramma sono quindi perpendicolari.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
