Proporzionalità diretta, inversa e dipendenza lineare

In questo appunto di fisica descriviamo due concetti fondamentali per la comprensione di molte leggi soprattutto di tipo sperimentale. Spieghiamo la proporzionalità diretta, la proporzionalità inversa e la dipendenza lineare tra due grandezze fisiche. Vediamo insieme le equazioni che caratterizzano questo tipo di legame tra grandezze fisiche, il loro significato nel piano cartesiano e alcuni esempi.

Proporzionalità diretta

Ricordiamo dalla geometria che due insiemi di grandezze sono direttamente proporzionali se si verificano due condizioni particolari:
Elementi di due insiemi si trovano in corrispondenza biunivoca fra loro
Il rapporto fra due qualsiasi grandezze del primo insieme è uguale al rapporto fra le corrispondenti grandezze del secondo insieme.
Ad esempio sono insiemi di grandezze proporzionali il peso e il costo di una merce, gli archi di una circonferenza e gli angoli al centro corrispondenti, gli spazi percorsi e i tempi impiegati a percorrerli nel moto uniforme.
Quando due insiemi di grandezze sono direttamente proporzionali, i rapporti fra le misure di due elementi che si corrispondono sono tutti uguali. Il numero costante che esprime questi rapporti e la costante di proporzionalità.
Dunque in generale possiamo affermare che: due grandezze sono direttamente proporzionali se comunque esse variano, il rapporto tra i valori che esse assumono resta costante, e questo valore è espresso dalla costante di proporzionalità.
Se indichiamo le due grandezze generiche con ed e, con indichiamo la costante, la relazione che esprime il legame di proporzionalità diretta è la seguente:

In questa relazione riconosciamo l’equazione di una generica retta passante per l’origine:

Possiamo quindi dire che l’equazione della retta passante per l’origine è il modello di proporzionalità diretta. Il coefficiente angolare di una retta rappresenta la sua pendenza; la pendenza è costante come k.
Per ulteriori approfondimenti su come calcolare la pendenza di una retta vedi qua

Significato e valori della costante di proporzionalità diretta

La costante di proporzionalità, al pari del coefficiente angolare può avere sia segno positivo che segno negativo, questo dipende dai quadranti del piano cartesiano attraversati dalla retta.
Se la costante k è positiva, la retta è crescente, questo significa che la retta è situata nel primo e nel terzo quadrante del piano.
Se la costante k è negativa, la retta è decrescente, questo significa che la fretta e situata nel secondo e nel quarto quadrante del piano.
Esempi di leggi di proporzionalità diretta:

• [math]y=2x[/math]
  : la relazione dice che la grandezza y è il doppio della grandezza x, la costante di proporzionalità è k=2
• [math]y=5x[/math]
  : la relazione dice che la grandezza y è il quintuplo della grandezza x, la costante di proporzionalità è k=5
• [math]y=\frac{1}{2}x[/math]
  : la relazione dice che la grandezza y è la metà della grandezza x, la costante di proporzionalità è
  [math]k={1\over 2}[/math]

Per ricavare la variabile x bisogna dividere y per la costante k:

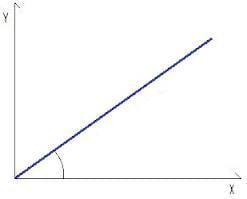
Nella figura seguente riportiamo un esempio di retta passante per l’origine che rappresenta una relazione di proporzionalità diretta.

Proporzionalità inversa

Due grandezze sono inversamente proporzionali quando al loro variare il prodotto rimane costante.

in cui

è la costante di proporzionalità.

Nel piano cartesiano la relazione di proporzionalità inversa è rappresentata da una iperbole equilatera se il valore di k è positivo i rami dell’iperbole si trovano nel primo e nel terzo quadrante. Nel primo quadrante le 2 variabili x e y sono entrambe positive, nel terzo quadrante le due variabili sono entrambe negative e il prodotto risulta sempre positivo.
Se la costante è negativa i due rami della funzione si trovano nel secondo e nel quarto quadrante. In questo caso le due grandezze

e sono sempre discordi.
Vediamo come ricavare ciascuna delle due variabili:

Per calcolare x:

Per calcolare y:

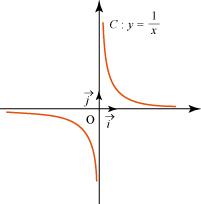
Riportiamo un esempio del grafico di una relazione di proporzionalità inversa, in cui il valore della costante è 1.

Per ulteriori approfondimenti sulla definizione dell’iperbole vedi qua

Dipendenza lineare

Due grandezze sono linearmente dipendenti se la relazione che le lega è esprimibile attraverso una funzione del tipo:

L’equazione rappresenta una retta del piano cartesiano non passante per l’origine. I parametri che la caratterizzano sono due il coefficiente angolare

e l’ordinata all’origine o intercetta, rappresentata dal termine .
Il parametro

[math]q[/math]

indica dove la retta interseca l’asse delle ordinate, infatti si chiama anche intercetta.
Il parametro indica sempre il coefficiente angolare o la pendenza.
Anche per questo tipo di relazione il segno di dà informazioni sulla della funzione.
Se la costante è positiva, abbiamo una funzione crescente.
Se la costante è negativa, abbiamo una funzione decrescente.
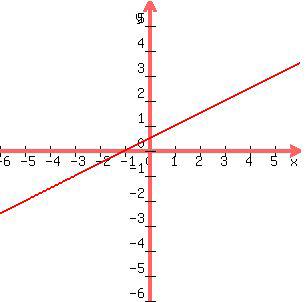
In figura abbiamo un esempio di legge di dipendenza lineare:

Per ulteriori approfondimenti sulle funzioni crescenti decrescenti e punti stazionari vedi qua

Come calcolare la proporzionalità diretta, inversa e lineare con la calcolatrice scientifica

Spieghiamo la procedura di calcolo da eseguire su una calcolatrice scientifica.
Passaggio #1

Collochiamoci nel menù

6: Statistics

Passaggio #2

Selezioniamo l’opzione 2.

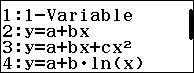
Passaggio #3

Inseriamo i valori della tabella assegnata.

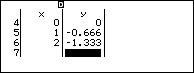
Passaggio #4

Digitiamo

La nostra calcolatrice genererà un codice QR.

Attraverso un semplice smarthphone, tramite l’app EDU+, potremo visualizzare l’andamento della funzione e identificare la proporzionalità.

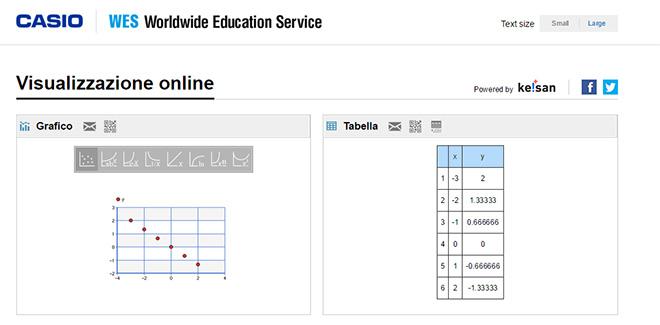
Passaggio #5

Selezionando l’icona

Ci verrà visualizzata la retta e la sua equazione generica. Dalla quale potremmo dedurre che si tratta di una dipendenza lineare.

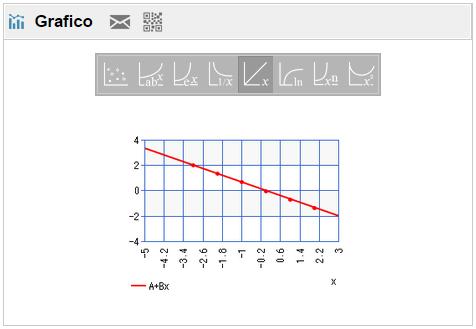
Passaggio #6

Per ricavare l’equazione digitiamo il tasto AC e poi OPTION

Seguito dall’opzione numero 4

Osserviamo che tale procedura è funzionale anche nel caso di altre leggi di proporzionalità