Equazione generale di un'iperbole

Equazione generale dell'iperbole e dell'iperbole traslata.

_stan
di _stan
Ominide
9 min. di lettura
Vota

Indice

  1. Iperbole traslata ed equazione generale dell'iperbole
  2. Altro materiale di supporto
  3. Esercizi proposti

Iperbole traslata ed equazione generale dell'iperbole

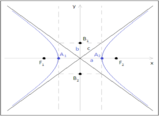
Equazione dell'iperbole traslata:

Consideriamo un'iperbole riferita ai propri assi, per esempio con i fuochi sull'asse delle ascisse. Se operiamo una traslazione del sistema di coordinate che porti gli assi ? ed ? in ?…2; ed ?…2; e, di conseguenza, il punto ? nel punto ?2;(?0,?0), anche l'iperbole risulterà traslata.

Avremo ottenuto così un'iperbole traslata, o come anche si suole chiamarla, riferita a rette parallele ai suoi assi.

Iperbole equilatera

Se l'equazione dell'iperbole originaria era

[math] H: x^2/a^2-y^2/b^2=1 [/math]

, l'iperbole traslata ?…2; si potrà scrivere come

[math] \displaystyle \begin{equation}H':\frac{(x-x_0)^2}{a^2}-\frac{(y-y_0)^2}{b^2}=1 \, \, \, \, \, \, \, \text{(1)}\end{equation} [/math]

Svolgendo i semplici conti algebrici che figurano nell'equazione precedente, otterremo poi

[math] \displaystyle b^2(x-x_0)^2-a^2(y-y_0)^2-a^2b^2=0 [/math]

[math] \displaystyle b^2(x^2+x^2_0-2xx_0)-a^2(y^2+y^2_0-2yy_0)-a^2b^2=0 [/math]

[math] \displaystyle b^2x^2-a^2y^2-2b^2x_0x+2a^2y_0y+b^2x^2_0-a^2y^2_0-a^2b^2=0 [/math]

Questa equazione può essere scritta più semplicemente nella forma

[math] \displaystyle \begin{equation}mx^2+ny^2+px+qy+r=0 \, \, \, \, \, \, \, \text{(2)}\end{equation} [/math]

avendo cura di fare le seguenti posizioni:

[math] \displaystyle m=b^2 \, \, \, \, \, n=-a^2 \, \, \, \, \, p=-2b^2x_0 \, \, \, \, \,q=2a^2y_0 [/math]

[math]r=b^2x^2_0-a^2y^2_0-a^2b^2 [/math]

Osservazione 1: In realtà perché l'equazione

[math](1)[/math]

possa essere scritta nella forma

[math](2)[/math]

non è necessario fare esattamente le posizioni appena citate, ma è sufficiente che i numeri ?,?,… siano proporzionali ai valori

[math] \displaystyle b^2, -a^2, \ldots [/math]

secondo un qualsiasi numero reale ? costante e non nullo. In particolare, ? non deve per forza essere positivo, se il ? scelto è negativo; un'uguale considerazione vale per ?.

Osservazione 2: Poiché abbiamo visto che l'equazione di qualunque iperbole traslata può scriversi nella forma

[math] (2)[/math]

, è logico domandarsi se qualsiasi equazione fatta come la

[math](2)[/math]

possa rappresentare un'iperbole. Già sappiamo che la risposta è negativa, in quanto per opportuni valori dei coefficienti ci è noto che l'equazione

[math](2)[/math]

può rappresentare un'ellisse. Inoltre, anche non conoscendo questa informazione sull'ellisse, possiamo fare questa semplice considerazione: non esiste valore reale ? tale che

[math] -ka^2 [/math]

e

[math] kb^2 [/math]

abbiano lo stesso segno, dunque ? ed ? devono quanto meno essere discordi, cioè avere segno opposto, affinché la

[math] (2) [/math]

rappresenti un'iperbole.

Equazione generale dell'iperbole: In questo paragrafo estenderemo i ragionamenti fatti nell' osservazione 2, col fine di scoprire quali condizioni deve soddisfare la

[math] (2) [/math]

per essere l'equazione di un'iperbole: giungeremo così all'equazione generale.

Iniziamo con il riscrivere la

[math] (2) [/math]

nel modo seguente:

[math] \displaystyle mx^2+ny^2+px+qy+r=0\rightarrow [/math]

[math] \displaystyle \rightarrow m\Big(x^2+\frac{p}{m}x\Big)+n\Big(y^2+\frac{q}{n}y\Big)+r=0 [/math]

Questo è lecito perché se ?=0 oppure ?=0 di certo l'equazione, non essendo più di secondo grado in una delle due variabili, non può rappresentare un'iperbole: i casi suddetti vanno perciò scartati. Poiché dall'osservazione 2 segue che ? ed ? devono essere discordi, essi si possono senz'altro prendere il primo positivo ed il secondo negativo cambiando in modo opportuno i segni dell'equazione. Ciò ci porta a dire che gli unici casi d'interesse sono quelli in cui

[math] m \gt 0 [/math]

ed

[math] n \lt 0 [/math]

.

Le somme in parentesi somigliano a dei quadrati di binomio, e lo diventano a patto di aggiungervi i termini

[math] \displaystyle \frac{p^2}{4m^2} [/math]

e

[math] \displaystyle \frac{q^2}{4n^2} [/math]

; adoperando questo metodo, detto del completamento dei quadrati, potremo scrivere

[math] \displaystyle m\Big(x^2+\frac{p}{m}x+\frac{p^2}{4m^2}\Big)-\frac{p^2}{2m}+n\Big(y^2+\frac{q}{n}y+\frac{q^2}{4n^2}\Big)-\frac{q^2}{4n}+r=0 [/math]

[math] \displaystyle m\Big(x+\frac{p}{2m}\Big)^2+n\Big(y+\frac{q}{2n}\Big)^2+r-\frac{p^2}{4m}-\frac{q^2}{4n}=0[/math]

Indicata poi con ? la somma algebrica

[math]\frac{p^2}{4m}+\frac{q^2}{4n}-r[/math]

, otterremo infine

[math] \displaystyle \begin{equation}\frac{\Big(x+\frac{p}{2m}\Big)^2}{1/m}-\frac{\Big(y+\frac{q}{2n}\Big)^2}{-1/n}=s \, \, \, \, \, \, \, \text{(3)}\end{equation}[/math]

Se

[math] s\gt 0 [/math]

, allora l'equazione

[math](3)[/math]

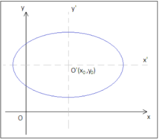
può essere riscritta nella forma seguente, che è quella di un'iperbole traslata con i fuochi giacenti su una parallela all'asse ?, centro

[math] \displaystyle O'\Big(-\frac{p}{2m}, -\frac{q}{2n}\Big)[/math]

, con

[math] \displaystyle a=\sqrt{\frac{s}{m}}[/math]

e

[math] \displaystyle (b=\sqrt{-\frac{s}{n}}[/math]

:

[math] \displaystyle \frac{\Big(x+\frac{p}{2m}\Big)^2}{s/m}-\frac{\Big(y+\frac{q}{2n}\Big)^2}{s/n}=1 [/math]

Se invece ?=0, allora la

[math](3)[/math]

diviene

[math] \displaystyle \frac{\Big(x+\frac{p}{2m}\Big)^2}{1/m}=\frac{\Big(y+\frac{q}{2n}\Big)^2}{-1/n}\rightarrow y+\frac{q}{2n}=\pm\sqrt{-\frac{m}{n}}\Big(x+\frac{p}{2m}\Big)[/math]

Ciò significa che l'iperbole degenera in due rette passanti per il suo centro

[math] \displaystyle O'\Big(-\frac{p}{2m}, \frac{q}{2n}\Big)[/math]

aventi coefficienti angolari

[math] \displaystyle \pm\sqrt{-m/n} [/math]

. Ricordando le definizioni di ? e ? date nel caso

[math] s \gt 0 [/math]

, però, scopriamo che

[math] \displaystyle \pm\sqrt{-m/n}=\pm b/a) [/math]

, col che le due rette sono gli asintoti dell'iperbole: ciò si riassume dicendo che in questo caso l'iperbole è degenere nei suoi asintoti.

Se infine abbiamo (slt 0), similmente a quanto visto nel caso 1 la

[math](3)[/math]

diventa

[math] \displaystyle -\frac{\Big(x+\frac{p}{2m}\Big)^2}{-s/m}+\frac{\Big(y+\frac{q}{2n}\Big)^2}{s/n}=1 [/math]

ovverosia, posti

[math] \displaystyle a=\sqrt{-\frac{s}{m}}[/math]

e

[math] \displaystyle b=\sqrt{\frac{s}{n}} [/math]

e avendo cura di cambiare i segni all'equazione,

[math] \displaystyle \frac{\Big(x+\frac{p}{2m}\Big)^2}{a^2}-\frac{\Big(y+\frac{q}{2n}\Big)^2}{b^2}=-1 [/math]

Questa è l'equazione di un'iperbole traslata i cui fuochi sono disposti verticalmente.

Da questo ragionamento deduciamo che l'equazione

[math] \displaystyle mx^2+ny^2+px+qy+r=0 [/math]

è l'equazione generale di un'iperbole se e solo se ? ed ? sono discordi, cioè

[math] mn \lt 0 [/math]

, e inoltre

[math] \displaystyle \frac{p^2}{4m}+\frac{q^2}{4n} \ne r[/math]

.

Osservazione 3: Ogni qual volta abbiamo posto ? e ? pari a certe radici quadrate, ci siamo sempre accertati di prendere i loro radicandi in maniera tale da risultare positivi. Ciò può essere facilmente verificato, ricordando che nel nostro caso il numero ? è sempre negativo.

Altro materiale di supporto

Videolezione sull'iperbole equilatera

Esercizi proposti

  1. Calcola l'equazione dell'iperbole equilatera, riferita agli asintoti, che stacca sulla retta di equazione
    [math] y=2x+1 [/math]
    una corda che misura
    [math] \displaystyle \frac{7}{2}\sqrt{5} [/math]
  2. Determina l'equazione dell'iperbole equilatera, riferita agli asintoti, tangente alla retta di equazione
    [math] y=5x-10 [/math]

Trovi uno spunto per le soluzioni nel forum di Matematicamente.it.

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Help (321322)
_stan di filo.22

Aiuto urgente per compiti
_stan di anitaminardi1987

Problema con potenze
_stan di gagix12

I migliori insegnanti di Matematica

Giovanni

Giovanni C.

Supertutor
Percorsi
Verificato

Insegnante di Aiuto tesi, Contabilità e bilancio, Controllo di gestione, Diritto

a partire da 20 €/ora
most booked
Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Mostra altri Tutor