In questo appunto di algebra troverai una spiegazione ampia sulla procedura di risoluzione delle disequazioni esponenziali. Per ciascuno dei seguenti casi: con la stessa base, con base differente, risolvibili mediante logaritmi, e risolvibili mediante metodo di sostituzione, ci sono degli esempi numerici svolti, per fissare al meglio le regole teoriche.

Indice
- Disequazioni esponenziali
- Disequazioni esponenziali in cui primo e secondo termine hanno la stessa base
- Esempi svolti del tipo con la stessa base
- Disequazioni esponenziali i cui termini non hanno la stessa base
- Esempi di disequazioni risolte con logaritmi
- Disequazioni esponenziali da risolvere con un'incognita ausiliaria (detto anche metodo della sostituzione)
Disequazioni esponenziali
Una disequazione esponenziale è innanzi tutto una disequazione in cui l'incognita "x" compare come esponente.Esistono per la verità anche disequazioni esponenziali in cui la "x" non compare solo come esponente. Ma in quel caso le disequazioni risultano molto complesse, e la loro risoluzione è possibile solo attraverso un metodo grafico. Ragion per cui, esse non verranno trattate nel presente appunto.
Per risolvere le disequazioni esponenziali occorre avere molto ben presenti:
1) Le proprietà delle potenze;
2) Le caratteristiche e proprietà dei logaritmi;
3) Le regole per risolvere le disequazioni.
Se questi tre argomenti non fossero chiari, si consiglia di riguardarli bene, al fine di poter comprendere a pieno tutti i passaggi che conducono alla risoluzione di una disequazione esponenziale. Trattandosi di argomenti non difficili ma comunque tali da richiedere trattazioni specifiche a parte, nel presente appunto essi verranno per forza di cose dati per scontati.
Per ulteriori approfondimenti sul metodo grafico vedi qua
Disequazioni esponenziali in cui primo e secondo termine hanno la stessa base
Nel più semplice dei casi, una disequazione esponenziale è già nella forma canonica:
Dove: f(x) e g(x) sono due funzioni della variabile reale “x” incognita.
Come si vede, le due potenze che costituiscono primo e secondo termine della disuguaglianza hanno la stessa base.
Per poter risolvere questo tipo di disequazione, occorre tenere presenti due cose:
Primo, che, essendo disequazioni, ad esse possono essere applicate (e devono essere applicate) tutte le regole che normalmente si utilizzano per risolvere le disequazioni.
Secondo, trattandosi di disequazioni esponenziali, occorre tenere a mente quali sono le proprietà delle potenze.
Questo naturalmente vale se le due basi "a" sono uguali e se sono maggiori di 1.
Nel caso in cui le basi fossero minori ad 1, la regola vale ancora, ma la relazione va invertita:
Esempi svolti del tipo con la stessa base
Esempio 1Supponiamo di avere la seguente disequazione:
Apparentemente, sembra non essere una disequazione esponenziale, perchè non compare nella forma in cui solitamente siamo abituati a vederla. Ma la possiamo trasformare in pochi passaggi, operando sulla radice quadrata. Ricordiamo che questo operatore rappresenta una potenza ad esponente fratto.
Cioè:
Come si vede, l'abbiamo ridotta ad una equazione esponenziale, ossia caratterizzata da una base comune(2) e da due funzione di "x" in esponente.
Poichè 2>1, da quanto abbiamo detto prima possiamo scrivere per gli esponenti che:
...che è una banale disequazione di primo grado facile da risolvere:
Cambiamo di segno. Ricordiamo che nelle disequazioni il cambiamento di segno comporta l'inversione del simbolo della disequazione.
Questa semplice soluzione è la soluzione della complessa disequazione di partenza.
ESEMPIO 2:
Svolgiamo ora 1:00 disequazione esponenziale con una base inferiore ad 1:
Uniformiamo le basi ai due membri :
La funzione esponenziale con base positiva è minore di uno è una funzione decrescente perciò dobbiamo invertire la relazione tra gli esponenti.
Cambiamo di segno. Come detto in precedenza, nelle disequazioni il cambiamento di segno comporta l'inversione del simbolo della disequazione.
Quindi:
...costituisce la soluzione della disequazione di partenza.
Per semplicità abbiamo sempre utilizzato delle f(x) e g(x) di primo grado. Le funzioni presenti negli esponenti possono essere di varia natura anche funzioni trascendenti del tipo funzioni goniometriche. Ovviamente cambia la natura delle disequazioni associate alla relazione tra gli esponenti e quindi anche la loro complessità, resta il fatto che la procedura è la stessa.
Per approfondimenti sulla funzione esponenziale vedi qua
Disequazioni esponenziali i cui termini non hanno la stessa base
In molti casi, però, primo e secondo termine della disuguaglianza non hanno la stessa base. Cioè la disequazione esponenziale si presenta nella forma:
In questo caso, il metodo di risoluzione è completamente differente dal precedente. Infatti per arrivare alla soluzione sarà necessario utilizzare i logaritmi.
Sarà dunque necessario avere molto ben presente la definizione di logaritmo quale operazione inversa dell'elevamento a potenza...
"Il logaritmo di un certo numero a in una base b (dove a e b sono entrambi reali e positivi e b è diverso da 1) è quel numero a cui si deve elevare la base b per ottenere come risultato il numero a".
...e tutte le proprietà che li riguardano:
Proprietà 1: Il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori.
Proprietà 2: Il logaritmo di un quoziente è uguale alla differenza fra il logaritmo del dividendo e quello del divisore.
Proprietà 3: Il logaritmo di una potenza è uguale al prodotto dell'esponente per il logaritmo della base di detta potenza.
Proprietà 4: Il logaritmo di un radicale è uguale al quoziente fra il logaritmo del radicando e l'indice del radicale. Detto molto più semplicemente:
Qualora infatti capitasse di dover risolvere una disequazione esponenziale in cui il primo e il secondo membro abbiano basi differenti, occorre attuare la seguente trasformazione:
In questo "specchietto" la base del logaritmo è 10, e solitamente è proprio la base che viene utilizzata per attuare la trasformazione. Tuttavia non esiste una regola fissa su quale debba essere la base dei logaritmi da utilizzare. Qualora l'esercizio risultasse semplificato, è possibile in realtà adottare qualunque tipo di base (positiva e diversa da 1).
Sarà a questo punto possibile giungere alla soluzione applicando le proprietà dei logaritmi sopra citate.
Per ulteriori approfondimenti sulle disequazione risolvibili mediante logaritmi vedi qua
Esempi di disequazioni risolte con logaritmi
Non c'è dubbio che la base del primo membro (2) sia diversa da quella del secondo (3). Adottiamo dunque la trasformazione appena vista:
A questo punto procediamo a semplificare la disequazione utilizzando le proprietà dei logaritmi:
Ora, nell'esercizio abbiamo adottato 10 come base per i nostri logaritmi. Ma in questo particolare caso non si è trattato di una scelta intelligente. Questo per nessun'altra ragione se non perchè -in questo particolare caso- scegliendo un'altra base è possibile un'ulteriore semplificazione.
Se infatti scegliamo come base 2 anziché 10 (e abbiamo detto che è una modifica che ci è perfettamente lecito fare)...
...la nostra disequazione diviene:
E più oltre non è possibile procedere.
In virtù di quanto appena detto, qualora il secondo termine si presentasse in questa forma più semplice:
...la trasformazione da eseguire sarà la seguente:
Se a>1:
Se a>0 e a:
E poichè:
Se a>1:
Se a>0 e a:
Disequazioni esponenziali da risolvere con un'incognita ausiliaria (detto anche metodo della sostituzione)
Certe disequazioni esponenziali hanno una struttura particolare, diversa da quella che abbiamo visto finora. Consistono cioè nella somma di più esponenziali. Queste disequazioni, per poter essere risolte, necessitano di una tecnica particolare, detta "dell'incognita ausiliaria" o più comunemente "della sostituzione".Tale metodo, sebbene non complesso, non sarà trattato in questi appunti. Ci si limita a dire che, grazie ad esso, è possibile trasformare una disequazione esponenziale in una sola disequazione di secondo grado. Risolvendo la disequazione di secondo grado sarà possibile pervenire alla soluzione dell'equazione esponenziale.


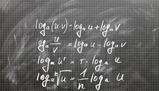





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo