Definizione di logaritmo: regole e formule

Appunto di matematica riguardante il concetto di logaritmo. Definizione, logaritmo naturale, logaritmo in base 10 ed alcuni esempi di calcolo di logaritmi.

stan.author
di stan.author
Ominide
10 min. di lettura
Vota

In questo appunto approfondiremo il concetto di logaritmo. Ne riprenderemo la definizione, vedremo alcuni importanti logaritmi, come quello naturale, che ha per base il numero di Nepero, e quello decimale, cioè in base 10. Inoltre, dopo aver dato un'occhiata ai grafici della funzione logaritmica, ci concentreremo su alcuni esempi di calcolo. Definizione di logaritmo: regole e formule articolo

Indice

  1. Definizione generale di logaritmo
  2. Definizione di logaritmo naturale o neperiano
  3. Definizione di logaritmo decimale o di Briggs
  4. Osservazioni
  5. Esempi elementari di calcolo di logaritmi

Definizione generale di logaritmo

Dati due numeri reali
[math]a>0[/math]
e
[math]b>0[/math]
,
[math]b \ne 1[/math]
si definisce logaritmo di base
[math]b[/math]
e argomento
[math]a[/math]
l'esponente da attribuire alla base
[math]b[/math]
per ottenere una potenza uguale all'argomento
[math]a[/math]
.

Ciò si scrive nella forma:

[math] x = \log_b a \Leftrightarrow b^x=a [/math]

Per esempio, proviamo a calcolare:

[math] \log_3 9 [/math]

.

Dobbiamo, cioè trovare il logaritmo in base 3 del numero 9. Per fare ciò dobbiamo porci la domanda: quale esponente devo assegnare alla base 3 per avere come risultato il numero 9.

Cioè, quale numero va messo al posto del punto interrogativo in:

[math] 3^? = 9 [/math]

Basta conoscere un po' di aritmetica di base per sapere che il numero cercato è 2.

Per cui possiamo scrivere che:

[math] \log_3 9 = 2[/math]

Oppure, possiamo chiederci, quanto vale

[math] \log_2 \frac{1}{8} [/math]

. Dobbiamo cioè risolvere:

[math] 2^? = \frac{1}{8} [/math]

Qui il discorso si complica un po' ma, ricordando che

[math] a^{-n} = \frac{1}{a^n} [/math]

concludiamo che l'esponente cercato è

[math] -3 [/math]

.

E dunque:

[math] \log_2 \frac{1}{8} = -3 [/math]

.

Ricorda anche due cose molto importanti.

Qualsiasi sia la base del logaritmo, se l'argomento è uguale ad 1, il valore del logaritmo sarà sempre zero. Infatti, qualsiasi numero elevato alla potenza 1 restituisce zero.

[math] \log_a 1 = 0[/math]

Se la base e l'argomento del logaritmo sono uguali, il risultato del logaritmo è sempre 1.

[math] \log_a a = 1 [/math]

Definizione di logaritmo naturale o neperiano

Alcuni logaritmi sono più utilizzati di altri, per cui acquistano dei nomi particolari. Uno di questi, forse il più importante, è il logaritmo che ha per base il numero
[math]e[/math]
. Il numero
[math]e[/math]
(o numero di Nepero) è un numero irrazionale, che vale:
[math] e = 2,71828 \, 18284 \, 59045 \, 23536 \dots [/math]
Un logaritmo la cui base è il numero di Nepero
[math]e[/math]
è detto logaritmo naturale o neperiano.

Per esso valgono le solite considerazioni:

[math] \log_e 1 = 0 [/math]

[math] \log_e e = 1 [/math]

Definizione di logaritmo decimale o di Briggs

Un altro logaritmo che viene spesso utilizzato è il logaritmo con base 10, detto anche logaritmo decimale.

Il logaritmo decimale è molto utilizzato per via del fatto che il numero 10 è la base del nostro sistema di numerazione.

[math] \log_{10} a = b \leftrightarrow 10^b=a [/math]

Il logaritmo decimale è noto anche con il nome di logaritmo di Briggs, dall'omonimo matematico britannico e, oltre ad indicarsi con il solito simbolo

[math] \log_{10} a = b [/math]
si può spesso trovare con l'iniziale maiuscola
[math] \text{Log} a = b [/math]
.

Osservazioni

Osservazione 1: Quando si dà una nuova definizione occorre sempre controllare che essa non sia contraddittoria. Nella definizione, viene detto che il logaritmo è precisamente quell'esponente da attribuire alla base
[math]b[/math]
per ottenere il numero
[math]a[/math]
; ciò presuppone che esista uno e un sol numero con tale proprietà. Effettivamente ciò corrisponde a verità, in quanto la funzione esponenziale di base
[math]b[/math]
è iniettiva, e quindi non esistono due
[math]x[/math]
diversi tali che
[math]x^b=a[/math]

Definizione di logaritmo

Osservazione 2: Dalla definizione di logaritmo, risulta che la base

[math]b[/math]
di un logaritmo deve consistere in un numero reale positivo differente da 1. Questa richiesta, a prima vista complicata, è facilmente spiegata osservando che, sempre per la definizione, deve valere

[math]b^x=a[/math]
: visto allora che
[math]b[/math]
deve essere anche la base di una funzione esponenziale, i valori negativi vanno eliminati a causa di come è definita quest'ultima.

Se invece fosse

[math]b=1[/math]
, avremmo che
[math]a=1^x=1[/math]
indipendentemente dal valore di
[math]x[/math]
, ovvero il nostro logaritmo si ridurrebbe alla funzione
[math]y=1[/math]
. Posto allora
[math]b>0[/math]
,
[math]b>1[/math]
può risultare o
[math]b>1[/math]
o
[math]0 > b >1[/math]
; i due grafici possibili in questi due casi per la funzione
[math]y=\log_b a[/math]
sono rappresentati nelle immagini precedenti.

Osservazione 3: La definizione di logaritmo

[math] \log_b a[/math]
richiede esplicitamente che risulti
[math]a > 0[/math]
. Ciò è dovuto alla definizione di logaritmo e alle proprietà della funzione esponenziale. Visto che infatti deve risultare
[math]b^x=a[/math]
e che la funzione esponenziale di base
[math]b[/math]
assume valori solo in
[math]\mathbb{R}^+[/math]
, necessariamente il valore di
[math]a[/math]
sarà positivo.

Osservazione 4: Il legame tra funzione esponenziale e logaritmo si può anche visualizzare nel modo che segue.
Si consideri il grafico già noto relativo alla funzione esponenziale di base

[math]b[/math]
(nell'immagine seguente lo si è rappresentato in rosso e si è scelto
[math]b > 1[/math]
) e la bisettrice del primo e terzo quadrante (in viola nel grafico). Riflettendo detto grafico rispetto alla retta data si ottiene il nuovo grafico in blu: esso è il grafico della funzione
[math]y=\log_b a[/math]
, ovvero del logaritmo.

Le proprietà dell'esponenziale valgono riflesse per il logaritmo: se l'esponenziale:

  • è definita su tutto
    [math]\mathbb{R}[/math]
    ,
  • assume valori in
    [math]\mathbb{R}^+[/math]
    ,
  • passa per il punto
    [math](0, 1)[/math]
  • tende a
    [math]0^+[/math]
    per
    [math]x \rightarrow -\infty [/math]

il logaritmo:

  • assume valori in tutto
    [math]\mathbb{R}[/math]
  • è definito su
    [math]\mathbb{R}^+[/math]
  • passa per il punto
    [math](1, 0)[/math]
  • tende a
    [math]-\infty[/math]
    per
    [math]x \rightarrow 0^+[/math]

In particolare ciò significa che, poiché l'esponenziale possiede un asintoto orizzontale, il logaritmo ne ha uno verticale.

Un legame di questo tipo tra i grafici di queste due funzioni è dovuto al fatto che esse sono una la funzione inversa dell'altra. Nella figura in basso puoi osservare entrambi i tipi di grafici logaritmici.

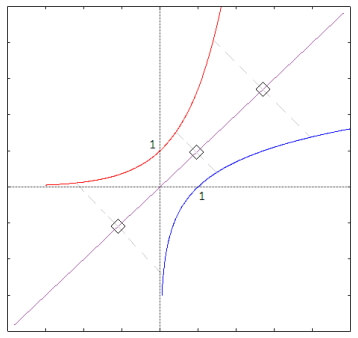
Grafici delle funzioni esponenziale e logaritmo

Per ulteriori approfondimenti sulla funzione logaritmica vedi anche qua

Esempi elementari di calcolo di logaritmi

Esempio 1: Proviamo a calcolare il valore di
[math]x=\log_b 1[/math]
. Come richiesto dalla definizione di logaritmo, per risolvere questo problema dovremo trovare quel valore, che esiste ed è unico in virtù dell'osservazione 1, tale che
[math]b^x=1[/math]
.
Indipendentemente da quale sia la base
[math]b[/math]
, sappiamo che elevandola alla 0 otterremo 1, cioè
[math]b^0=1[/math]
,
[math]\forall b[/math]
. Quindi il risultato sarà
[math]\log_b 1=0[/math]
. In effetti, l'osservazione 4 ci assicurava già che il grafico del logaritmo passa per il punto
[math](1,0)[/math]
quale che sia la base
[math]b[/math]
, cosicché il risultato era in effetti banale.

Esempio 2: Calcoliamo adesso

[math]\log_b b[/math]
. Adoperando ancora la definizione, sappiamo che il numero ricercato deve essere tale che
[math]b^x=b[/math]
. Com'è noto già dalle proprietà delle potenze, l'elevazione di un numero qualsiasi alla 1 ci restituisce il numero stesso; dunque certamente
[math]\log_b b=1[/math]
per ogni
[math]b[/math]
.

Esempio 3: Utilizzando sempre lo stesso metodo, è possibile verificare i seguenti risultati:

[math] x=\text{Log} 1000\rightarrow x=log_{10}1000\rightarrow 10^x=1000=10^3\rightarrow x=3 [/math]

[math] x=ln \sqrt{e} \rightarrow x = log_e \sqrt{e} \rightarrow e^x = \sqrt{e} = e^{1/2} \rightarrow x = frac{1}{2} [/math]

Esempio 4: Proviamo infine a calcolare il valore di

[math]x=\\log_{2}3[/math]
. Se come al solito ricorriamo alla definizione, scopriamo solo che
[math]2^x=3[/math]
.
Ciò non ci è di grande aiuto, visto che non conosciamo alcun numero
[math]x[/math]
"semplice" che verifichi questa equazione.

Infatti, comunque eleviamo 2 a un numero naturale, otteniamo sempre un numero pari, ed essendo 3 dispari l'uguaglianza non può mai valere.

D'altro canto la funzione esponenziale è definita su tutto

[math]\mathbb{R}[/math]
, quindi una soluzione deve necessariamente esistere. Visto che non la conosciamo con precisione, possiamo quanto meno tentare di approssimarla: visto allora che
[math]2 > 3 > 4[/math]
, è lecito scrivere:

[math]2^1 > 2^x>2^2[/math]

Questo, unitamente al fatto che la funzione esponenziale è crescente, ci assicura che la

[math]x[/math]
da noi ricercata appartiene all'intervallo
[math](1, 2)[/math]
; in effetti usando una calcolatrice scientifica risulta che
[math]x\approx 1.585[/math]
, e quindi la nostra stima è corretta.

Per ulteriori approfondimenti sui logaritmi, vedi anche qua

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Help (321322)
stan.author di filo.22

Aiuto urgente per compiti
stan.author di anitaminardi1987

Problema con potenze
stan.author di gagix12

I migliori insegnanti di Matematica

Giovanni

Giovanni C.

Supertutor
Percorsi
Verificato

Insegnante di Aiuto tesi, Contabilità e bilancio, Controllo di gestione, Diritto

a partire da 20 €/ora
most booked
Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Mostra altri Tutor