Concetti Chiave
- La forza è una grandezza fisica misurata in Newton, rappresentata come vettore con intensità, direzione e verso.
- La forza risultante su un corpo è la somma vettoriale di tutte le forze applicate, considerando segni e angoli fra di esse.
- Le leve sono sistemi in cui forze applicate in punti diversi sono descritte da relazioni proporzionali tra bracci e forze.
- La formula delle leve, F1 * d1 = F2 * d2, aiuta a determinare il punto di applicazione della forza risultante.
- Nel problema esempio, la forza risultante è 300N e si trova più vicina alla forza di maggiore intensità, F2.
In questo appunto viene risolto un problema sulle forze e sulle leve, dato che il problema richiede il calcolo della forza risultante e il punto di applicazione di una delle due forze applicate, è utile ripassare brevemente il concetto e la definizione di forza, di forza risultante e di leva.
Indice
La forza: definizione e somma di forze
Ogni volta che proviamo a muovere un oggetto, ogni volta che eseguiamo un movimento del corpo, stiamo applicando una forza, la forza quindi è una grandezza che non è possibile definire in modo semplice ma è una grandezza con la quale abbiamo sempre a che fare e di cui possiamo notare gli effetti.
La forza viene misurata in Newton (N).
Un Newton è definito come la forza che deve essere applicata ad un corpo con una massa di 1kg per imprimergli un’accelerazione di
Il Newton è un’unità di misura derivata in quanto può essere espressa in funzione dei Kg, dei metri e dei secondi; il Newton infatti corrisponde a:
Esistono diversi tipi di forze, alcuni esempi sono la forza peso, la forza di attrito, la forza elastica…
Ogni forza può essere rappresentata con un vettore: l’intensità della forza è relazionata al modulo o lunghezza del vettore mentre la direzione e il verso del vettore corrispondono alla direzione e al verso della forza applicata.
Se un corpo è sottoposto a più forze, è possibile definire la forza risultante (R) come la somma vettoriale di tutte le forze applicate.
Ricordiamo che la somma vettoriale tiene conto del segno del vettore (se si sommano due forze con verso opposto è necessario introdurre un segno meno in una delle due forze), e tiene conto dell’angolo compreso tra le due forze (in questo caso è utile scomporre le forze lungo gli assi di un piano cartesiano precedentemente definito).
Per ulteriori approfondimenti sui vettori e sulla loro somma vedi anche qua
Le leve: definizione ed equazioni fondamentali
Nel caso in cui due o più forze sono applicate in punti diversi di un oggetto è importante considerare il punto di applicazione della forza.
Definiamo il braccio (d) di una forza la distanza del punto di applicazione della forza da un punto considerato l’origine del sistema di riferimento.
In genere un corpo a cui vengono applicate due o più forze in punti di applicazione differenti prende il nome di leva.
Le leve sono descritte da un’equazione fondamentale che mette in relazione i bracci delle forze con le forze applicate, la relazione è la seguente:
Tale relazione può essere riarrangiata e riscritta sottoforma di divisioni:
Tale relazione è un esempio di proporzione quindi se si conoscono 3 quantità e si vuole conoscere la quarta, è possibile utilizzare le proprietà delle proporzioni per trovare la grandezza richiesta.
L’equazione riportata per le leve può essere utilizzata anche per trovare la posizione della forza equivalente che deve essere applicata per generare gli stessi effetti di due forze applicate su un corpo con i punti di applicazione a una distanza d.
In tal caso la forza risultante sarà in una posizione più vicina alla forza che ha maggiore intensità; nella formula sopra riportata le distanze
e
sono le distanze dei punti di applicazione rispettivamente delle forze
ed
.
Se le due forze applicate hanno la stessa intensità, la forza risultante avrà un’intensità doppia rispetto alle singole forze e avrà un punto di applicazione che si trova esattamente a metà rispetto ai punti di applicazione delle singole forze.
Problema e risoluzione
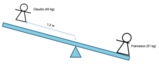
Una barra rigida è sottoposta all’azione di due forze
ed
, entrambe le forse hanno direzione verso l’alto e sono applicate in due punti che si trovano ad una certa distanza.
Inoltre la distanza fra il punto di applicazione della risultante e quello della forza
è
.
- Trovare il valore della risultante.
- A quale distanza dalla forza [math]F_1[/math]risulta applicata la forza risultante?
Svolgimento
Per trovare il valore della risultante, cioè la forza totale, basta fare la somma delle due forze, poiché queste sono parallele concordi (entrambe hanno uguale direzione e uguale verso):
Il secondo punto chiede di trovare la distanza della forza risultante dalla forza
Chiamiamo
la distanza tra la forza
e la forza risultante e
la distanza tra la forza
e la forza risultante (dai dati forniti dal testo
).
Il punto di applicazione della forza risultante è sempre più vicino alla forza caratterizzata da una maggiore intensità, perciò in questo caso il punto di applicazione della forza risultante sarà più vicino alla forza
.
Applichiamo quindi la proporzione che mette in relazione i bracci delle forze e le intensità delle forze applicate:
Sostituiamo i valori con i dati forniti dal problema:
Esplicitiamo
, la quantità che ci viene richiesta:
Per ulteriori approfondimenti su alcuni tipi di forze vedi anche qua
Domande da interrogazione
- Qual è la definizione di forza e come si misura?
- Come si calcola la forza risultante quando un corpo è sottoposto a più forze?
- Cosa rappresenta il braccio di una forza in una leva?
- Qual è l'equazione fondamentale delle leve e come si utilizza?
- Come si risolve il problema della barra rigida con due forze applicate?
La forza è una grandezza che si manifesta quando si tenta di muovere un oggetto o si esegue un movimento. È misurata in Newton (N), definito come la forza necessaria per imprimere un'accelerazione di 1 m/s² a un corpo di 1 kg.
La forza risultante è la somma vettoriale di tutte le forze applicate. Si tiene conto del segno del vettore e dell'angolo tra le forze, scomponendole lungo gli assi di un piano cartesiano.
Il braccio di una forza è la distanza tra il punto di applicazione della forza e un punto considerato l'origine del sistema di riferimento. È fondamentale per calcolare l'equilibrio delle leve.
L'equazione fondamentale delle leve è [math]F_1 \cdot d_1 = F_2 \cdot d_2[/math]. Si utilizza per trovare la posizione della forza equivalente che genera gli stessi effetti di due forze applicate su un corpo.
Si sommano le forze parallele concordi per ottenere la forza totale: [math]F_{tot} = 100 N + 200 N = 300 N[/math]. Poi, si applica la proporzione [math]F_2 : F_1 = d_1 : d_2[/math] per trovare la distanza [math]d_1[/math] dalla forza [math]F_1[/math], risultando in [math]d_1 = 1,2 m[/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
