Vettori e calcolo vettoriale
Per quanto concerne la rappresentazione matematica delle grandezze fisiche, si distinguono:
- le grandezze scalari (come la massa), corrispondenti a semplici valori algebrici dotati di segno;
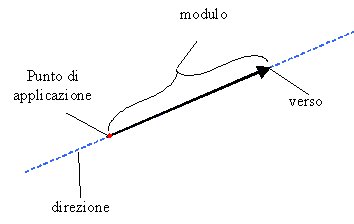
- le grandezze vettoriali (come la velocità), associate a un orientamento e, per questo, descritte da vettori.
I vettori si possono combinare tra loro secondo le particolari regole dell'algebra vettoriale.
Collocato un vettore in un sistema (qualsiasi) di coordinate ortogonali, è possibile scomporlo rispetto agli assi di quest'ultimo.
Nel caso più generale (cioè nello spazio) un vettore è completamente determinato dalle sue proiezioni sugli assi x, y, z, che ne costituiscono le componenti vettoriali.
Tali componenti sono vettori, di verso concorde all'orientamento del vettore che costituiscono.
Detti versori (o vettori unitari) i vettori i, j, k di intensità pari a 1, configurati secondo gli assi del sistema, le componenti vettoriali sono date dal prodotto di questi ultimi con i fattori che ne determinano il modulo, detti componenti scalari.
NOTA 1 - I versori costituiscono una base per la rappresentazione di qualunque vettore.
NOTA 2 - Solitamente, i vettori si configurano secondo un sistema di coordinate simmetrico all’area di lavoro (che si tratti di un foglio o dello schermo di un computer). In realtà, qualunque sistema ruotato di ϕ gradi è ugualmente adatto a rappresentare uno stesso vettore, semplicemente attraverso componenti diverse. Esistono infiniti sistemi di coordinate; conoscendo la misura degli angoli che li differenziano è possibile rappresentare uno stesso vettore rispetto a ciascuno di essi (trasporto per parallelismo).
Ogni vettore forma con le sue componenti dei triangoli rettangoli, pertanto sono applicabili le relazioni trigonometriche seguenti (si considera il caso di un vettore bidimensionale di modulo v, ruotato di un angolo θ rispetto all'asse delle ascisse x):
La somma di due o più vettori si può ottenere, geometricamente, attraverso le seguenti regole.
- Regola del parallelogramma: la somma di due vettori applicati a uno stesso punto corrisponde alla diagonale del parallelogramma che essi definiscono con le rispettive proiezioni.
- Regola della poligonale: la somma di due o più vettori applicati in sequenza corrisponde al vettore che congiunge il punto di applicazione del primo all'estremità dell'ultimo.
NOTA - La somma di vettori è un'operazione commutativa e associativa, cioè non dipende in alcun modo dall'ordinamento o dal raggruppamento degli addendi.
La differenza di due o più vettori risulta analogamente alla somma, a partire dalla definizione di vettore opposto.
Dato un vettore v, si definisce vettore opposto il vettore -v di pari intensità e direzione, ma di verso contrario.
La differenza di due vettori si ricava, quindi, dalla somma del primo all'opposto del secondo.
Sono ugualmente applicabili le regole geometriche.
Il prodotto sv tra un vettore v e una grandezza scalare s restituisce un nuovo vettore così caratterizzato:
- l'intensità del nuovo vettore è pari al prodotto algebrico tra il termine scalare s e il modulo di v;
- la direzione del nuovo vettore è pari alla direzione del vettore v;
- il verso del nuovo vettore è pari al verso di v se il termine scalare s è positivo, contrario altrimenti.
Dati due vettori, si definisce prodotto scalare (o prodotto interno) l'operazione corrispondente al prodotto algebrico tra i loro moduli e il coseno dell'angolo ϕ che sottendono.
Per definizione, il prodotto scalare ha le seguenti proprietà:
- restituisce sempre un risultato scalare;
- può essere riscritto come il prodotto algebrico tra il modulo del primo vettore e la componente scalare del secondo lungo la direzione del primo (o viceversa);
- se i due vettori considerati sono sovrapposti l'angolo ϕ che sottendono misura 0°, nel qual caso [math]\cos \phi=1[/math]e il prodotto scalare è pari al prodotto algebrico dei rispettivi moduli;
- se i due vettori considerati sono ortogonali l'angolo ϕ che sottendono misura 90° o 270°, nel qual caso [math]\cos(\phi)=0[/math]e il loro prodotto scalare è necessariamente nullo.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo