Nella geometria piana ci sono tre teoremi che valgono per i triangoli rettangoli e la conoscenza di questi teoremi risulta molto utile nella risoluzione di problemi geometrici di vario tipo. Si tratta del teorema di Pitagora e dei due teoremi di Euclide. In questo appunto proponiamo un problema per il cui svolgimento sono richiesti proprio i due teoremi di Euclide. Ripassiamo insieme gli enunciati dei teoremi e poi passiamo allo svolgimento del problema proposto.
Primo teorema di Euclide
I due teoremi di Euclide e il teorema di Pitagora affermano delle equivalenze tra superfici piane ovvero tra quadrati e rettangoli costruiti sui lati dei triangoli rettangoli.
Entrambi i teoremi hanno anche una formulazione più semplice che sfrutta le proprietà delle proporzioni.
Enunciato del primo teorema di Euclide: in un triangolo rettangolo il quadrato costruito su uno dei suoi cateti è equivalente al rettangolo avente per lati l'ipotenusa e la proiezione del cateto sull'ipotenusa stessa.
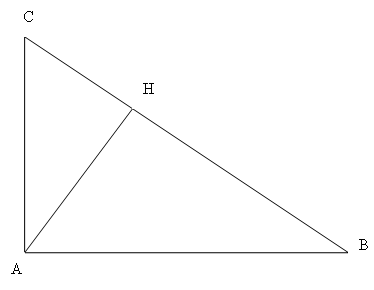
Sia dunque ABC un triangolo rettangolo con l’angolo retto nel vertice A come quello in figura sopra.
L’altezza relativa all’ipotenusa di questo triangolo è il segmento AH.
I segmenti AB e AC sono i due cateti.
I due segmenti in cui l’ipotenusa resta divisa dal punto H, BH e HC sono le proiezioni dei due cateti.
Consideriamo il cateto minore AB, l'area del quadrato costruito su questo cateto è:
Il rettangolo che ha per dimensioni la proiezione di questo cateto sull’ipotenusa BH e l'ipotenusa stessa BC, ha area:
Per il primo teorema abbiamo:
Oppure:
Vediamo ora l'altra formulazione del primo teorema del tutto equivalente a questa qui.
In un triangolo rettangolo, ciascun cateto è il medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.
Se facciamo riferimento sempre alla figura in alto possiamo scrivere:
Applicando ora la proprietà fondamentale delle proporzioni, per la quale il prodotto dei medi è uguale al prodotto degli estremi otteniamo l'equivalenza precedente:
Se in un problema è nota la misura dell’ipotenusa e la proiezione di un cateto su di essa, si può calcolare la misura del cateto estraendo la radice quadrata del secondo membro dell'uguaglianza:
Secondo teorema di Euclide
Il secondo teorema di Euclide mette in relazione l'altezza di un triangolo rettangolo, relativa all'ipotenusa, con entrambe le proiezioni dei due cateti sull’ipotenusa stessa.
Abbiamo sempre un triangolo rettangolo con angolo retto in A e questa volta abbiamo disegnato il quadrato sull'altezza e il rettangolo sull'ipotenusa.
Il teorema afferma che: in un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sulla ipotenusa.
L’area del quadrato è:
L’area del rettangolo è
Per il teorema è sempre:
Ovvero:
Anche per il secondo teorema di Euclide vale sempre la formulazione con le proporzioni.
Diremo in questo caso che l’altezza del triangolo rettangolo relativa all’ipotenusa è medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa stessa. In simboli matematici, abbiamo:
Da cui sempre per la proprietà fondamentale delle proporzioni ricaviamo nuovamente la relazione di equivalenza tra le due superfici:
Con il secondo teorema di Euclide è possibile calcolare l'altezza di un triangolo rettangolo relativa all'ipotenusa, quando sono note le misure delle proiezioni dei due cateti su di essa.
Teorema di Pitagora
In ogni triangolo rettangolo la somma dei quadrati costruiti sui cateti è equivalente al quadrato costruito sull’ipotenusa.
Questo teorema è sicuramente il più utilizzato non solo nella geometria ma anche in algebra nonché in fisica.
La sua dimostrazione è molto semplice perché si sfrutta il primo teorema di Euclide applicandolo ad entrambi i cateti.
Osservando la figura sono stati indicati con
i quadrati costruiti rispettivamente sul cateto AB, sul cateto AC e sull’ipotenusa BC.
Per dimostrare che la somma dei quadrati
e
è equivalente proprio al quadrato
costruito sull’ipotenusa, basta prolungare la semiretta che contiene l'altezza AH in modo tale da dividere il quadrato di lato BC in due rettangoli.
Per il primo teorema di Euclide applicato al cateto AB sappiamo che il quadrato costruito su di esso è equivalente al rettangolo
.
Sempre per il primo teorema di Euclide applicato al cateto AC, il quadrato costruito su di esso è equivalente al rettangolo
.
Poiché somme di figure equivalenti sono equivalenti, risulta:
Ovvero
Che è la tesi del Teorema.
Problema svolto
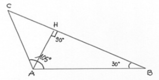
Testo del problema
In un triangolo rettangolo sono note le misure dei cateti e della ipotenusa, esse sono rispettivamente
- [math]AB=20cm[/math]
- [math]AC=15cm[/math]
- [math]BC=25cm[/math]
- [math]AH= ?[/math]
Avendo a disposizione questi dati calcolare l’altezza relativa all’ipotenusa.
Svolgimento
Il problema può essere risolto in maniera molto semplice calcolando prima l’area del triangolo rettangolo come semiprodotto delle misure dei due cateti poi, utilizzando la formula inversa dell'area si effettua il doppio prodotto di questa misura e lo si divide per l'ipotenusa in questo modo si ottiene la misura dell'altezza.
Da cui
Volendo utilizzare i teoremi visti, avremmo proceduto come segue.
Con il primo teorema di Euclide, applicato ad uno dei due cateti, possiamo calcolare la misura della sua proiezione, e per differenza con la misura dell'ipotenusa calcoliamo anche l'altra proiezione.
Applichiamo il teorema al cateto AB, la sua proiezione misura:
La proiezione dell’altro cateto è data da:
Ora che sono note le misure delle due proiezioni possiamo applicare il secondo teorema di Euclide per determinare la misura dell’altezza AH:
- [math]AH=\sqrt{BH\cdot HB}[/math]
- [math]AH=\sqrt{16cm\cdot 9cm}[/math]
- [math]AH=\sqrt{144cm^2}=12cm[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
