Il seguente appunto contiene un problema svolto che richiede il perimetro e l'area di un triangolo rettangolo dato uno dei cateti e l'ipotenusa. Affronteremo il problema svolto in due modi: il primo modo con l'utilizzo della geometria euclidea, nel secondo modo procederemo, invece, per via trigonometrica.
Indice
Area triangolo rettangolo
Useremo in questo problema, oltre alla "classica" formula dell'area (ossia
) la formula trigonometrica per il calcolo dell'area: ossia, data l'ipotenusa di un triangolo rettangolo e un cateto ad essa adiacente, l'area del triangolo rettangolo è data dal semiprodotto tra l'ipotenusa, il cateto e il seno dell'angolo compreso tra l'ipotenusa e il cateto. In formule,
.
Testo del problema svolto
Si calcoli il perimetro e l'area di un triangolo rettangolo che ha l'ipotenusa che misura
e il cateto minore che misura
.
Metodo 1: Teorema di Pitagora
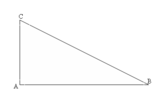
D'ora in poi supporremo il triangolo avente l'angolo retto in
.
Di conseguenza, l'ipotenusa sarà
, mentre gli altri due cateti saranno
e
.
Dati
- [math]AC = 35 \text{cm}[/math]
- [math]BC = 21 \text{cm}[/math]
Svolgimento
Per risalire all'area del triangolo
, è necessario conoscere la misura dei due cateti in modo tale da poter applicare la formula dell'area (cioè l'area è uguale al semiprodotto tra base e altezza), ma di cateti ne abbiamo solo uno. Applichiamo pertanto il Teorema di Pitagora per calcolare il cateto rimanente
. Si ottiene quindi:
.
Ora abbiamo dati sufficienti per risalire sia al perimetro che all'area.
Calcolo del perimetro
Per definizione, il perimetro è dato dalla somma di tutti i lati che compongono il triangolo.
.
Calcolo dell'area
Notoriamente l'area è data dal semiprodotto tra base e altezza.
Pertanto, applicando la formula, si ottiene:
.
Metodo 2: Trigonometria
Supponiamo gli stessi dati di prima. Come detto nel primo paragrafo, possiamo dire che l'area di un triangolo è data dal semiprodotto tra i due lati e il seno dell'angolo compreso. Intanto, scriviamo nuovamente i dati.
Dati
- [math]AC = 35 \text{cm}[/math]
- [math]BC = 21 \text{cm}[/math]
Svolgimento:
È necessario trovare quindi il seno dell'angolo
. Per fare ciò, utilizzeremo il Teorema dei Seni.
Possiamo stabilire la proporzione:
.
Essendo inoltre il triangolo rettangolo, sappiamo che
. Da questo ricaviamo che
per le proprietà delle proporzioni.
Tuttavia, noi cerchiamo il seno dell'angolo
. Possiamo ricavarcelo con il seguente ragionamento: sappiamo intanto che
sono complementari. È inoltre noto che negli angoli complementari seno e coseno si "scambiano", cioè avremo
e
.
Quindi
, in sostanza ci tocca determinare
. Dalla relazione fondamentale della trigonometria (cioè il seno al quadrato più il coseno al quadrato fa sempre 1) troviamo che
( \widehat{ACB} )[/math]
.
Calcolo dell'area
Ora possiamo affermare che l'area del triangolo in questione è data da
ove, sostituendo, si ottiene:
.
Per approfondimenti su questa formula, vedi anche qua.
Calcolo del perimetro
Abbiamo ora determinato l'area senza usare il cateto mancante, che tuttavia ora va determinato. Per definizione di seno e coseno avremo che
.
Quest'ultimo seno è già stato calcolato prima. Pertanto
.
Si sarebbe potuto determinare l'altro cateto alternativamente. Conoscendo già l'area e un cateto, ci sarebbe bastato fare:
.
Il perimetro
è quindi dato da
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
