In un triangolo ABC l'angolo a è 105° e quello B è 30. Sapendo che l'altezza AH è di 20cm, trova il perimetro e l'area.
Soluzione
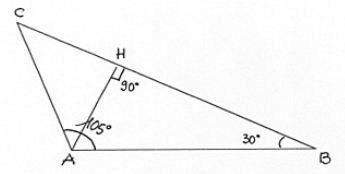La somma degli angoli interni di un triangolo è sempre
[math]180°[/math]
. Nel triangolo
[math]AHB[/math]
, l'angolo in [math]hat(A) = 60°[/math]
Poiché tutto l'angolo in
[math]hat(A)[/math]
, cioè [math]hat(CAB)[/math]
, vale [math]105°[/math]
, si ha [math]hat(CAH) = 45°[/math]
. Consideriamo ora il triangolo
[math]CHA[/math]
. Poiché [math]hat(H) = 90°[/math]
, [math]hat(A) = 45°[/math]
. allora anche [math]hat(C) = 45°[/math]
. In definitiva,
[math]CAH[/math]
è metà di un quadrato, [math]AHB[/math]
è metà di un triangolo equilatero.
[math]\bar(AH) = 20 cm = \bar(CH)[/math]
. Applichiamo ora il teorema di Pitagora per ricavare
[math]CA[/math]
:[math]\bar(CA) = \sqrt{400+400} cm = \sqrt(800) cm = 28.28 cm text(circa)[/math]
Passiamo ora al triangolo
[math]AHB[/math]
Si ha:
[math]\bar(AB) = 2cdot \bar(AH) = 40 cm[/math]
. Applichiamo di nuovo il teorema di Pitagora:
[math]\bar(HB) = \sqrt{40^2-20^2} = \sqrt(1200) = 34.64 cm text(circa)[/math]
Il perimetro del triangolo
[math]ABC[/math]
si ottine da[math]40 cm + 28.28 cm + 20 cm + 34.64 cm[/math]
L'area si ottiene da
[math]((20+34.64)cdot 20)/2 cm^2[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
