Funzioni goniometriche e loro inverse

In questo appunto di Matematica si affrontano le funzioni trigonometriche principali attraverso la loro definizione ed il loro grafico su piano cartesiano, con una introduzione agli angoli.

Angoli, archi e loro misure

Chiameremo angolo quella parte di piano individuata da due semirette uscenti da uno stesso punto O, incluse tali semirette.
Il punto O costituisce il vertice dell’angolo, mentre le due semirette ne costituiscono i lati:
un angolo piatto ha i lati che sono uno l’opposto dell’altro; un angolo nullo ha i lati coincidenti.
Chiameremo angolo convesso, quell’angolo che non contiene al suo interno il prolungamento dei lati e si dirà concavo in caso contrario.
Un arco di circonferenza è quella parte di circonferenza inclusa in un angolo al centro della circonferenza stessa:
i punti A e B di intersezione dei lati dell’angolo al centro con la circonferenza si chiamano estremi dell’arco.
Ad angoli al centro della circonferenza uguali corrispondono archi uguali e viceversa.
L’unità di misura degli angoli può essere:

• il grado
• il radiante.

Il grado è definito come la 360^a parte di un angolo giro; la sessantesima parte del grado si chiama minuto primo e la sessantesima parte di quest’ultimo si chiama minuto secondo.
Il radiante o angolo radiante è l’angolo al centro di una circonferenza di raggio arbitrario, che sottende un arco di lunghezza uguale al suo raggio.
La definizione di radiante deriva dal fatto che in due circonferenze diverse, due archi, che corrispondono ad angoli al centro di uguale ampiezza, sono proporzionali ai rispettivi raggi:
dati gli archi l ed l’ che individuano lo stesso angolo al centro α si ha che

Facendo il rapporto membro a membro si ottiene la seguente relazione

da cui segue che se

allora

In particolare se le due circonferenze sono concentriche si arriva alla seguente conclusione:
se un angolo al centro di una circonferenza individua un arco lungo quanto il raggio, allora lo stesso angolo individua su qualsiasi altra circonferenza concentrica con la prima, un arco lungo quanto il raggio della circonferenza stessa.
Per la misura degli archi si mette in relazione la loro lunghezza con l’angolo al centro corrispondente:
fissato un sistema di misura, lo stesso numero che dà la misura di una arco di una data circonferenza, dà anche la misura del corrispondente angolo al centro; e viceversa.
Poiché la misura della lunghezza di una circonferenza di raggio r è data da

e tale lunghezza corrisponde ad un angolo al centro pari ad un angolo giro, pari a 360°, la formula che mette in relazione angoli in gradi ed angoli in radianti è data da:

dove

= angolo misurato in grado

= angolo in radianti
Infine diamo due importanti definizioni che ci serviranno per la misurazione degli angoli.
Definiamo angolo orientato, un angolo per cui si è stabilito quale dei due lati deve considerarsi come primo.
Dato un angolo orientato di vertice O, diremo che è positivo, quando è descritto dal lato origine (primo lato) mediante una rotazione antioraria attorno al punto O; lo chiameremo negativo, quando è descritto dal lato origine mediante una rotazione oraria attorno ad O.

Funzione seno e coseno

Si consideri una circonferenza goniometrica, ossia di raggio r = 1, ed un sistema di riferimento cartesiano Oxy con l’origine O coincidente con il centro della circonferenza.
Si consideri l’asse x come il primo lato di un qualunque angolo che individueremo tramite un punto P che si trova sulla circonferenza ed il secondo lato OP che tale punto forma tramite la sua congiungente con l’origine O.
Sia α tale angolo orientato positivo individuato dall’asse x e dal segmento OP.
Chiameremo seno dell’angolo orientato α, senα, l’ordinata del punto P.

Ossia essendo Q la proiezione ortogonale di P sull’asse x, chiameremo senα la grandezza espressa nel modo seguente:

Chiameremo coseno dell’angolo orientato α, cosα, l’ascissa del punto P. Ossia la grandezza espressa dalla seguente espressione:

Dalle precedenti definizioni date si arriva ad asserire che:
il seno ed il coseno di un dato angolo orientato α sono funzioni di tale angolo, cioè sono numeri reali che dipendono esclusivamente dall’ampiezza dell’angolo considerato.

Proprietà delle funzioni senα e cosα

La prima importante proprietà che lega la funzione seno alla funzione coseno è costituita dalla relazione fondamentale:
la somma dei quadrati del seno e del coseno di uno stesso angolo orientato è uguale ad uno

tale relazione la si ricava applicando il Teorema di Pitagora al triangolo rettangolo individuato dai punti OQP, retto in Q ed avente ipotenusa OP = 1.

da cui

La seconda importante proprietà di queste funzioni riguarda il loro segno.
Come è ben noto il piano cartesiano ortogonale individua quattro quadranti nello spazio.
Diremo che il seno di un angolo orientato è positivo se il secondo lato dell’angolo cade nel I o II quadrante (dove l’ordinata del punto P è positiva, QP > 0); diremo che è negativo se tale lato cade nel III o IV quadrante (dove l’ordinata di P è negativa, QP Diremo che il coseno di un angolo orientato è positivo se il suo secondo lato cade nel I o IV quadrante (dove l’ascissa di P è positiva, OP > 0); diremo che è negativo se tale lato si trova nel II o III quadrante (dove l’ascissa di P è negativa, OP Infine la terza importante proprietà delle funzioni seno e coseno è costituita dal fatto che il valore di tali grandezze oscilla fra -1 e +1:

assumendo i valori +1 e -1 per angoli particolari e fa sì che tali grandezze siano funzioni periodiche, ossia funzioni che dopo un dato periodo si ripetono uguali con le stesse caratteristiche.

Grafico delle funzioni seno e coseno

Analizziamo l’andamento del grafico di queste due funzioni trigonometriche considerando il punto P che si muove sulla circonferenza goniometrica di raggio r = 1, ed assumendo come punto iniziale quello in cui il punto P ha coordinate P = (1;0) ossia il punto in cui il segmento OP è allineato con l’asse delle x del sistema di riferimento cartesiano ortogonale.
Suddividiamo lo studio per quadranti:
I quadrante da 0° a 90° oppure da 0 a π/2 radianti.
II quadrante da 90° a 180° oppure da π/2 a π radianti.
III quadrante da 180° a 270° oppure da π a 3π/2 radianti.
IV quadrante da 270° a 360° oppure da 3π/2 a 2π radianti.
La funzione seno, nel punto iniziale P = (1;0), ha valore nullo poiché QP = 0. Se P comincia a muoversi sulla circonferenza in senso antiorario, l’angolo α comincia a crescere e ad assumere valori positivi; il segmento QP (ordinata di P), da zero, assume valori crescenti. L’andamento della curva seno è sinusoidale.
Se α = π/4 (45°), il segmento QP che rappresenta il seno dell’angolo vale

, ossia coincide col lato del quadrato di diagonale pari ad 1 (OP = 1).
Nel punto in cui α = π/2 (90°), il punto P ha coordinate P = (0;1), quindi QP = 1, quindi senα = 1.
Se P continua a spostarsi sulla circonferenza (sempre in senso antiorario), entra nel II quadrante. I valori del segmento QP, ordinata di P, dal valore 1, iniziano a diminuire riprendendo tutti i valori che aveva assunto nel I quadrante, ma stavolta decrescendo verso lo zero. Valore che il seno assume quando l’angolo α = π, P ha le seguenti coordinate P = (-1;0) e senα = 0, poiché QP = 0 nuovamente.
Nel III quadrante il valore del segmento QP, da zero assume valori negativi, fino a quando per α = 3π/2, si ha QP = -1, ossia senα = -1 ed il punto P ha coordinate P = (0;-1)
Nel IV quadrante i valori dell’ordinata di P, da -1, tornano a crescere verso lo zero. Valore raggiunto quando α = 2π, quindi senα = 0 e P sarà di nuovo nel punto di partenza, P = (1;0).
Da questo punto in poi la funzione seno si ripete allo stesso modo, per cui possiamo affermare che il periodo della funzione seno è T = 2π.
La funzione coseno, nel punto iniziale P = (1;0), ha valore uno poiché OQ = 1. Se P comincia a muoversi sulla circonferenza in senso antiorario, l’angolo α cresce e ad assume valori positivi; il segmento OQ (ascissa di P), da uno, assume valori decrescenti. L’andamento della curva coseno è anch’essa sinusoidale.
Se α = π/4 (45°), il segmento OQ che rappresenta il coseno dell’angolo vale

, ossia coincide col lato del quadrato di diagonale pari ad 1 (OP = 1).
Nel punto in cui α = π/2 (90°), il punto P ha coordinate P = (0;1), quindi OQ = 0, quindi cosα = 0.
Se P continua a spostarsi sulla circonferenza (sempre in senso antiorario), entra nel II quadrante. I valori del segmento OQ, ascissa di P, dal valore 0, continuano a diminuire riprendendo tutti i valori che aveva assunto nel I quadrante, ma stavolta con segno negativo, fino ad arrivare a -1. Valore che il coseno assume quando l’angolo α = π, P ha le seguenti coordinate P = (-1;0) e cosα = -1, poiché OQ = -1.
Nel III quadrante il valore del segmento OQ, da -1, torna a crescere verso lo zero, fino a quando per α = 3π/2, si ha OQ = 0, ossia cosα = 0 ed il punto P ha coordinate P = (0;-1)
Nel IV quadrante i valori dell’ascissa di P, da 0, assumono valori positivi e tornano a crescere verso 1. Valore raggiunto quando α = 2π, quindi cosα = 1 e P sarà di nuovo nel punto di partenza, P = (1;0).
Da questo punto in poi la funzione coseno si ripete allo stesso modo, per cui possiamo affermare che il periodo della funzione coseno è T = 2π.
Oltre alle due principali funzioni goniometriche, seno e coseno, esistono anche altre funzioni derivate dalle precedenti (seno e coseno).
Una di queste è la funzione tangente dell’angolo orientato α, che definiamo come il rapporto fra il seno dell’angolo α ed il suo coseno:

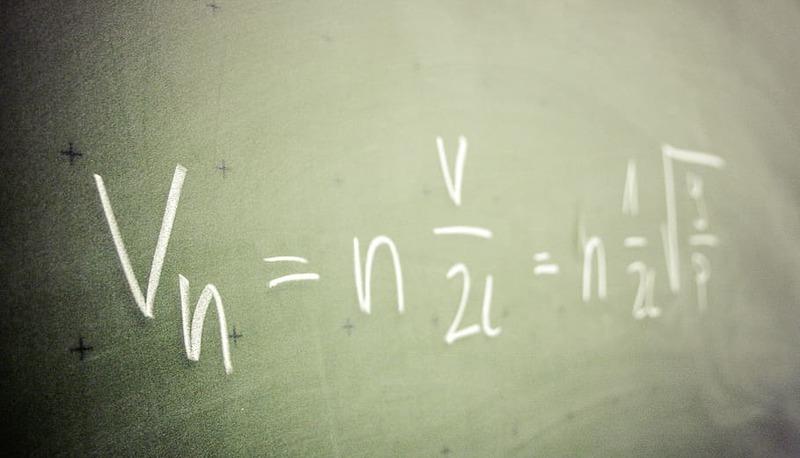
avente periodo T = π.
Tale funzione non è definita quando cosα = 0, ossia quando α = π/2 oppure α = 3π/2. Per tali valori di α corrispondono a due asintoti verticali per la funzione tangente ed essa tende ad infinito.

Funzioni trigonometriche inverse

Dalla teoria delle funzioni sappiamo che una funzione è invertibile se e solo se è biiettiva (ossia monotona).
Sia la funzione seno, che la funzione coseno non sono funzioni biiettive e per definirne le funzioni inverse dovremo restringere gli intervalli di studio ad intervalli in cui queste due funzioni sono monotone. Per la funzione y = senx restringiamo il dominio all’intervallo [-\frac{π}{2};\frac{π}{2}], in modo tale che
y = senx risulti biiettiva e quindi invertibile.
Chiameremo arcoseno la funzione inversa del seno e diremo che:
dati i numeri reali x ed y, con

e

diciamo che y è l’arcoseno di x se x è il seno di y e lo indichiamo con y = arcsenx.
Per la funzione coseno restringiamo il dominio all’intervallo [0,π] e chiameremo la sua funzione inversa arcocoseno. In base a tali ipotesi si ha che:
dati i numeri reali x ed y, con

e

, diremo che y è l’arcocoseno di x se x è il coseno di y e lo indicheremo con:
y = arcocosx.
Per la funzione tangente, dati i numeri reali x ed y, con x ∈ R e (

), diremo che y è l’arcotangente di x se x è la tangente di y e la indicheremo con
y = arctgx.

Per ulteriori approfondimenti sulle funzioni trigonometriche vedi anche qua