Funzioni goniometriche: seno e coseno

In quest'appunto troverai alcune definizioni riguardanti le funzioni goniometriche e in particolare seno e coseno. Inoltre, è presente un elenco delle ampiezze fondamentali.

Cosa sono le funzioni seno e coseno e a cosa servono

Le funzioni goniometriche sono delle funzioni aventi come argomenti un angolo. Esse sono particolarmente utili nello studio di fenomeni aventi un preciso periodo (come un moto sinusoidale) oppure nell'analisi dei triangoli.

Seno e coseno sono due funzioni goniometriche fondamentali e servono a convertire il valore di un angolo, sia esso in radianti o in gradi, in un numero puro. Nei triangoli rettangoli, il seno e il coseno di determinati angoli possono essere messi in relazione con la lunghezza dell'ipotenusa e la lunghezza dei cateti. In questo modo, è possibile calcolare un lato o l'ipotenusa avendo nota l'altra lunghezza e un angolo.
In particolare nei triangoli rettangoli si ha che:

• la misura del cateto maggiore o del cateto minore è pari al prodotto tra il seno dell'angolo opposto e la lunghezza dell'ipotenusa
• la misura di un cateto è pari al prodotto tra la tangente dell'angolo opposto e la lunghezza dell'altro cateto

Seno e coseno sono delle funzioni periodiche: ciò significa che i valori si ripetono con un certo periodo. In particolare, il periodo del seno e del coseno è pari a

. Questa caratteristica può essere evidenziata in modo chiaro anche dal metodo di rappresentazione mediante circonferenza goniometrica.
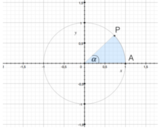
La circonferenza goniometrica è una circonferenza realizzabile sul piano cartesiano avente centro nell'origine degli assi e raggio unitario. Tale figura può essere utilizzata al pari di un goniometro: fissando una delle due semirette dell'angolo sull'asse delle e prolungando l'altra semiretta si intercetta la circonferenza in un punto.

Cos'è il seno: definizione e simbolismo

Il seno di un angolo, per definizione, è l'ordinata di un punto che giace sulla circonferenza goniometrica. Il punto è il punto d'incontro tra il raggio vettore e la circonferenza goniometrica. Ruotando attorno al punto forma un angolo a con il punto che è l'origine degli archi. L' ordinata del punto rappresenta quindi l'ordinata di .
I valori che il seno di un angolo può assumere posso essere rappresentati da questa dicitura:
{}
e sono quindi maggiori del valore e minori del valore .

Cos'è il coseno: definizione e simbolismo

Il coseno di un angolo, per definizione, è l'ascissa di un punto che giace sulla circonferenza goniometrica. I valori che il seno di un angolo può assumere posso essere descritti da questa dicitura:
{}
e quindi anche il coseno assume valori maggiori di e minori di .

I valori fondamentali: la tabella di seno e coseno

Vi sono alcuni valori di seno e coseno noti particolarmente ricorrenti: utilizzare una tabella come la seguente può aiutare a velocizzare lo svolgimento di espressioni ed equazioni goniometriche.

Da questa tabella è possibile apprezzare chiaramente la periodicità delle due funzioni. Il valore

è infatti assunto dal seno quando e quando .

La relazione fondamentale fra seno e coseno

Seno e coseno sono legati fra loro da una relazione, detta "Prima relazione fondamentale". Essa risulta molto utile durante lo svolgimento di dimostrazioni, equazioni ed espressioni goniometriche perchè, grazie a questa relazione, basta avere il seno oppure il coseno, per ricavarsi l'altra funzione.

Secondo la prima relazione fondamentale si ha che:

.

Scrivendo le formule inverse, quindi, si ha ancora che:

Esempio commentato: svolgimento di un'equazione trigonometrica sfruttando i teoremi precedentemente citati

La prima relazione fondamentale tra seno e coseno può essere utilizzata per semplificare un'equazione trigonometrica.
Consideriamo l'equazione .
In essa possiamo riconoscere quattro quantità differenti: il quadrato della funzione seno (), la funzione coseno (), il quadrato della funzione coseno () e il valore 1.

L'equazione non può essere svolta direttamente per via della presenza dei quadrati. Dal teorema precedentemente spiegato, però, sappiamo che

. La somma algebrica gode della proprietà commutativa, quindi posso riscrivere l'equazione in questo ordine:
.

Eseguendo un raccoglimento totale rispetto ai due termini, possiamo ancora scrivere:

da cui per la prima relazione fondamentale tra seno e coseno
.

Sommiamo algebricamente i termini simili e isoliamo a primo membro la funzione trigonometrica e al secondo membro il valore noto. Da questo si ottiene:

.

Dalla tabella dei valori noti illustrata nei paragrafi precedenti possiamo notare che l'angolo avente coseno pari a

è l'angolo piatto (). Per scrivere in maniera completa la soluzione bisogna aggiungere all'angolo individuato la periodicità, che nel caso delle funzioni seno e coseno è . Perciò la soluzione dell'equazione è .

Per ulteriori approfondimenti su seno e coseno vedi anche qui