Geometria analitica: equazione della circonferenza con centro nell'origine e raggio unitario

In questo appunto viene risolto l’esercizio che prevede di trovare l’equazione della circonferenza con centro nell’origine e con raggio unitario. Per comprendere meglio tale risoluzione viene proposto un breve ripasso sulle caratteristiche della circonferenza e sulla relativa equazione.

Circonferenza: caratteristiche ed elementi costitutivi

La circonferenza è definita come il luogo dei punti equidistanti da un punto caratteristico chiamato centro.
Gli elementi caratteristici della circonferenza sono quindi il centro e il raggio: il raggio è la distanza tra il centro e ogni punto che appartiene alla circonferenza.

Distanza tra due punti:

Dati due punti nel piano cartesiano

e

la distanza tra i due punti può essere calcolata tramite la seguente espressione:

Tale equazione può essere ricavata applicando il teorema di Pitagora alla differenza tra le ordinate e le ascisse dei due punti; utilizzando tale teorema possiamo trovare l’ipotenusa del triangolo che coincide proprio con la distanza tra i due punti.

Equazione analitica della circonferenza

Nel paragrafo precedente abbiamo definito la circonferenza come il luogo geometrico dei punti equidistanti dal centro; per costruire l’equazione che descrive tale figura possiamo proprio partire da questa caratteristica.
Ogni punto (x,y) che appartiene alla circonferenza ha la stessa distanza dal centro

Nel caso della circonferenza tale distanza coincide proprio al raggio perciò:

Se ora eleviamo al quadrato entrambi i membri si ottiene:

Tale equazione è proprio l’equazione analitica implicita che descrive una circonferenza con centro generico

Per ricavare l’equazione esplicita della circonferenza è necessario svolgere i termini al quadrato.
Ricordiamo che in questo caso è necessario svolgere il quadrato di un binomio che risulta essere uguale al primo termine al quadrato (

) + il doppio prodotto dei due monomi (

) + il secondo termine al quadrato (

).
Si ottiene:

Si portano tutti i termini da un lato dell’uguale e l’equazione esplicita della circonferenza che si ottiene è la seguente:

Se ora chiamiamo a,b,c i coefficienti rispettivamente della x, della y e del termine noto, otteniamo l’equazione generale esplicita della circonferenza:

Se ci viene fornita un’equazione esplicita è possibile risalire alle coordinate del centro

e alla misura del raggio utilizzando le seguenti formule:

Osservando le equazioni analitiche della circonferenza in forma implicita ed esplicita si può notare che in entrambe i termini con la x e la y al quadrato hanno coefficiente unitario.
La caratteristica fondamentale che deve avere un polinomio per poter rappresentare una circonferenza è quella di avere il termine con x al quadrato e il termine con le y al quadrato con gli stessi coefficienti.
In genere tale coefficiente è unitario però nei casi più generali tali coefficienti possono essere uguali ma diversi da 1, in questi casi si può risalire all’equazione esplicita della circonferenza dividendo sia a destra che a sinistra dell’uguale per il coefficiente dei termini al quadrato, in tal modo i coefficienti dei termini al quadrato si semplificano e risultano essere unitari.

Per ulteriori approfondimenti sul quadrato di un binomio vedi anche qua

Equazione della circonferenza con centro nell’origine e raggio unitario

Determiniamo l'equazione della circonferenza con centro nell'origine e raggio 1.

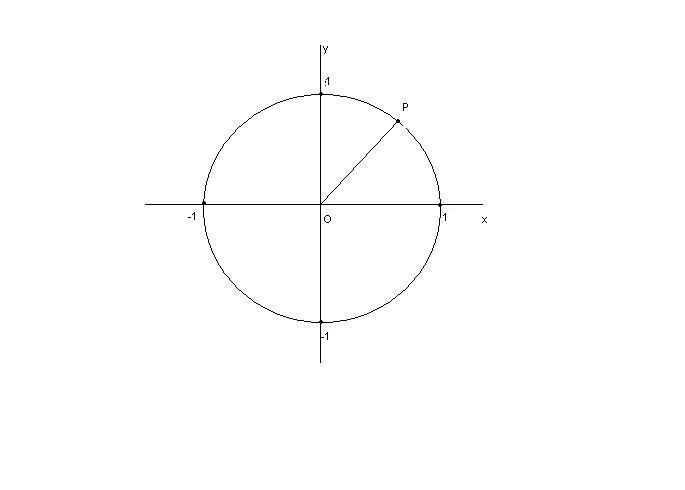
Svolgimento 1:
I punti appartenenti a questa circonferenza sono quelli aventi distanza dall'origine pari a 1,
cioè la circonferenza considerata è il luogo geometrico dei punti P del piano per cui si ha:

Indicando con (x,y) le coordinate del generico punto P e tenendo presente la seguente formula che esprime la distanza tra due punti nel piano cartesiano:

L'uguaglianza

può essere riscritta introducendo le coordinate del centro C(0,0) (ricordiamo che l’origine degli assi ha sia l’ascissa che l’ordinata nulle):

Perciò:

Elevando al quadrato ambo i membri dell'equazione si ottiene l’equazione implicita della circonferenza:

Se ora si portano tutti i termini da un lato dell’uguale otteniamo l’equazione esplicita della circonferenza:

Quest'ultima rappresenta l'equazione della circonferenza con centro nell'origine e raggio 1.

Svolgimento 2:
Al posto di ripercorrere il significato della circonferenza e le sue caratteristiche consideriamo subito l’equazione implicita della circonferenza:

Vogliamo trovare l’equazione della circonferenza con centro nell’origine perciò con

e con raggio unitario quindi r=1.
Sostituiamo tali valori nell’equazione implicita della circonferenza e otteniamo:

Eseguiamo i calcoli e otteniamo l’equazione implicita della circonferenza:

Se ora portiamo tutti i termini da un alto dell’uguale otteniamo l’equazione esplicita della circonferenza con centro nell’origine e raggio unitario:

La circonferenza con centro nell’origine e con raggio unitario è definita circonferenza goniometrica ed è un elemento fondamentale nell’ambito della geometria goniometrica che fa uso di funzioni goniometriche come la funzione seno e coseno.

Per ulteriori approfondimenti sulla circonferenza goniometrica vedi anche qua