di Anthrax606

Genius

5 min. di lettura

Vota 5 / 5

Distanza tra due punti in un piano cartesiano

Sia dato un piano cartesiano dove vi è disegnato un segmento

[math]AB[/math]

posto parallelamente all'asse delle

[math]y[/math]

Gli estremi del segmento

[math]AB[/math]

abbiano coordinate

[math]A=(-4;5),\ \ B=(-4;-3)[/math]

Chiamiamo le coordinate di ogni punto in questo modo:

A=(-4;5) -->

[math](x_{a};y_{a})[/math]

B=(-4;-3) -->

[math](x_{b};y_{b})[/math]

Essendo il segmento

[math]AB[/math]

parallelo all'asse delle

[math]y[/math]

allora quando andremo a calcolare, consideriamo solo i punti che

sono in coordinate

[math](y_{a};y_{b})[/math]

e le sottraiamo.

Logicamente andiamo a sottrarre la coordinata

[math]y_{b}[/math]

alla coordinata

[math]y_{a}[/math]

Quindi otteniamo:

[math]AB=\ |y_{a}-y_{b}|=\ |5-(-3)|cm=\ |5+3|cm=\ 8cm[/math]

Ora consideriamo un altro esempio:

Il segmento

[math]CD[/math]

questa volta,sarà parallelo all'asse delle

[math]x[/math]

Consideriamo le coordinate degli estremi:

[math]C=(-4;4)\ \ D=(5;4)[/math]

Chiamiamo le coordinate di ogni punto in questo modo:

C=(-4;4) -->

[math](x_{c};y_{c})[/math]

D=(5;4) -->

[math](x_{d};y_{d})[/math]

Essendo il segmento

[math]CD[/math]

parallelo all'asse delle

[math]x[/math]

andiamo

a considerare solo le coordinate in

[math]x[/math]

ossia:

[math](x_{c};x_{d})[/math]

In questo caso:

il punto

[math]D[/math]

si trova "più a destra" del punto

[math]C[/math]

Quindi bisogna sottrarre dalla coordinata

[math]x_{d}[/math]

la coordinata

[math]x_{c}[/math]

Dunque, andiamo a calcolare la misura del segmento

[math]CD[/math]

[math]CD=\ |x_{d}-x_{c}|=\ |5-(-4)|cm=\ |5+4|cm=\ 9cm[/math]

Andiamo ad esaminare l'ultimo caso. In questo caso il segmento

[math]EF[/math]

sarà posto obliquamente al piano cartesiano.

Consideriamo le coordinate degli estremi:

[math]E=(-5;-4)\ \ F=(2;6)[/math]

Chiamiamo le coordinate di ogni punto in questo modo:

E=(-5;-4) -->

[math](x_{e};y_{e})[/math]

F=(2;6) -->

[math](x_{f};y_{f})[/math]

Essendo il segmento

[math]EF[/math]

obliquo rispetto sia

all'asse delle

[math]x[/math]

che all'asse delle

[math]y[/math]

per calcolare la distanza tra i due punti, e quindi la lunghezza del

segmento, dobbiamo applicare una formula che ci permetterà di

calcolare quest'ultimo.

In questo caso, dobbiamo considerare sia le coordinate

[math]x[/math]

sia

le coordinate

[math]y[/math]

Non è importante l'ordine in cui vengono sottratti, perchè saranno

elevate al quadrato.

[math]EF=\sqrt{(x_{e}-x_{f})^{2}+(y_{e}-y_{f})^{2}}=\sqrt{(|-5-2|)^{2}+(|-4-6|)^{2}}cm=[/math]

[math]=\sqrt{(|-7|)^{2}+(|-10|)^{2}}cm=\sqrt{|49|+|100|}cm=\sqrt{|149|}cm=±12,21cm[/math]

In definitiva, dall'analisi dei tre casi precedenti possiamo dedurre

le seguenti regole generali.

Detti

[math]A(x_1,y_1),\ B(x_2,y_2)[/math]

i due punti di cui calcolare la

distanza si ha:

1) Se

[math]x_1=x_2[/math]

(punti su una retta parallela all'asse y)

[math]AB=|y_1-y_2|[/math]

2) Se

[math]y_1=y_2[/math]

(punti su una retta parallela all'asse x)

[math]AB=|x_1-x_2|[/math]

3) In generale

[math]AB=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\\[/math]

Punto medio di un segmento

Dati due punti di coordinate

[math]A(x_A,\,y_A)[/math]

[math]B(x_B,\,y_B)[/math]

il punto medio del segmento

[math]AB[/math]

ha banalmente coordinate:

[math]M\left(\frac{x_A + x_B}{2}, \; \frac{y_A + y_B}{2}\right)[/math]

Calcolare distanza tra due punti in un piano cartesiano utlizzando la calcolatrice scientifica Casio FX-991EX

Passaggio #1

Collochiamoci nel menù:

1 : Calculate

Passaggio #2

Inseriamo utilizzando in modo opportuno il comando alpha la relazione per il calcolo della distanza:

foto di passaggio #2

Passaggio #3

Digitiamo il comando CALC

E con il tasto cursore inseriamo i valori di A, B, C, D corrispondenti alle coordinate dei punti.

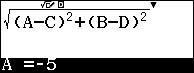
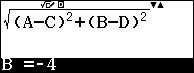
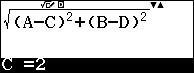
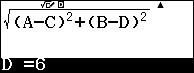
foto di operazione passaggio #3

Passaggio #4

Digitando il comando

otterremo la soluzione cercata.

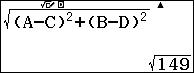
foto di operazione passaggio #4

Passaggio #5

Attraverso il comando:

potremo visualizzare la forma decimale.

foto di operazione passaggio #5

Osserviamo che tale procedura è funzionale anche nel caso di punti su una retta parallela all'asse x o y.

Qui di seguito il procedimento completo:

foto di procedimento completo

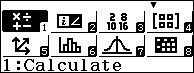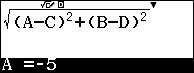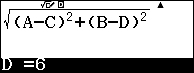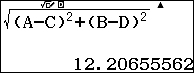
> > > Clicca qui e scopri tutte le funzioni della calcolatrice Casio FX-991EX!

Distanza tra due punti in un piano cartesiano

Appunti di matematica per le scuole superiori. Impareremo a calcolare la distanza tra due punti nel piano cartesiano e a il punto medio di un segmento sia con il metodo tradizionale che con la ca...

Distanza tra due punti in un piano cartesiano

Punto medio di un segmento

Calcolare distanza tra due punti in un piano cartesiano utlizzando la calcolatrice scientifica Casio FX-991EX

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Distanza tra due punti in un piano cartesiano

Punto medio di un segmento

Calcolare distanza tra due punti in un piano cartesiano utlizzando la calcolatrice scientifica Casio FX-991EX

Appunti correlati

Punti e rette nel piano cartesiano

Come calcolare l’area di un triangolo nel piano cartesiano

Piano cartesiano - Caratteristiche

Piano cartesiano - Parabola

Recensioni

Domande e risposte

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.