Goniometria e trigonometria

In questo appunto di matematica ci occuperemo della goniometria e della trigonometria, definendo le funzioni elementari e le regole fondamentali che legano tali funzioni ai lati di un triangolo.

Goniometria e trigonometria

La goniometria è quella parte della matematica che si occupa della definizione e della misura degli angoli e delle funzioni a questi associate (seno, coseno, tangente, ecc.).

In questa parte della matematica, oltre alle definizioni cui si è precedentemente accennato, vengono date delle formule che legano le funzioni goniometriche di più angoli a seconda della relazione che li interessa (come ad esempio fra gli angoli associati che sono archi differenti che hanno valori delle funzioni goniometriche uguali in valore assoluto).
La trigonometria studia le relazioni che legano le misure dei lati di un triangolo a quelle dei suoi angoli. Quindi in questa parte della matematica vengono elaborati dei teoremi nei quali i lati di un qualunque triangolo vengono messi in relazione ai suoi angoli interni.

Gli angoli

Definiamo angolo ciascuna delle due parti in cui un piano è diviso da due semirette che hanno origine in comune, comprese le semirette.
Il punto in comune alle due semirette che definiscono un angolo si chiama vertice, mentre le due semirette che lo definiscono sono dette lati.
A seconda della propria ampiezza diremo che un angolo è:

• nullo;
• giro;
• piatto;
• retto.

Diremo che un angolo è nullo quando i suoi lati sono coincidenti ed è formato dalla sola semiretta dei lati.
Diremo che un angolo è giro quando i suoi lati sono coincidenti ed è formato da tutti i punti del piano.
Diremo che un angolo è piatto se i suoi lati sono uno il prolungamento dell’altro.
Infine se due rette, intersecandosi, formano quattro angoli uguali, ciascuno di tali angoli viene chiamato retto.
La misura degli angoli avviene tramite due metodi principali:

• misura in gradi;
• misura in radianti.

Nel sistema sessagesimale si considera un angolo giro di 360°. Il grado viene definito come la 360-esima parte dell'angolo giro:
1°

di un angolo giro.
Ogni grado è suddiviso in 60 parti che prendono il nome di primo:
1° = 60’.
Il primo, a sua volta, è suddiviso in altre 60 parti che prendono il nome di secondo:
1’ = 60”.
Il radiante invece è la misura dell'angolo al centro che sottende un arco di lunghezza pari al centro della circonferenza, per cui l’angolo

si esprima come segue:

dove
l = lunghezza dell’arco
r = raggio della circonferenza.
La formula che ci permette il passaggio dal sistema dal sistema di misura sessagesimale a quello in radianti è la seguente:

dove

è langolo misurato in radianti
e

è l’angolo misurato in gradi.
In particolare si ha che:

Infine è bene precisare il concetto di angolo orientato. Nel caso in cui venga scelto un lato di un angolo come lato origine e venga fissato un senso di rotazione, allora l’angolo si dice orientato (l’altro lato viene chiamato lato termine). Diremo che un angolo orientato è positivo se è descritto da una rotazione oraria; mentre lo definiremo negativo quando la rotazione avviene in senso antiorario.

Funzioni goniometriche

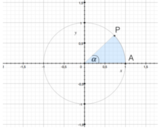
Si consideri il piano cartesiano ed una circonferenza avente centro nell’origine O nel piano cartesiano e raggio uguale ad uno, tale curva viene definita come circonferenza goniometrica, la cui equazione è la seguente:

Il punto di coordinate (1;0) viene chiamato origine degli archi. Tramite la circonferenza goniometrica si ha la possibilità di rappresentare gli angoli orientati, dove l’asse delle x viene scelto come lato origine.
Fissato un qualunque punto P sulla circonferenza goniometrica, sia H la sua proiezione ortogonale sull’asse x e sia

l’angolo che il raggio PO forma con l’asse delle x. Sia PHO il triangolo rettangolo, retto in H.
Definiamo seno dell’angolo

il rapporto fra il cateto PH (cateto opposto all’angolo) e l’ipotenusa OP:

Mentre definiamo coseno dell’angolo

il rapporto fra il cateto OH (cateto adiacente all’angolo) e l’ipotenusa OP:

Il seno ed il coseno di un angolo orientato

o, in modo del tutto analogo, come il rapporto fra i cateti PH e OH del triangolo rettangolo PHO, o ancora, come il rapporto fra il cateto opposto ed il cateto adiacente all’angolo:

ossia

A tale funzione si deve aggiungere la cotangente, definita come la reciproca della tangente:

Infine si hanno la funzione secante e la funzione cosecante:

Se il punto P, partendo dall’origine degli archi, si muove sulla circonferenza goniometrica in senso antiorario avremo che:
se

allora

poiché PH = 0
mentre

poiché OH = OP = 1.
Man mano che l’angolo

cresce PH aumenta di lunghezza, mentre OH diminuisce, questo significa che il seno dell’angolo cresce e quello del coseno diminuisce, finoa quando l’angolo

raggiunge il valore

Se

avremo che
PH = 1
OH = 0
Per cui

Se l’angolo

continua a crescere, il cateto PH decresce, mentre il cateto OH cresce in valore assoluto, ma con segno negativo. Quando

, avremo che

poiché PH = 0

poiché OH = -1
ossia il punto P ha coordinate (-1;0).
Se l’angolo

cresce ulteriormente, il cateto PH cresce in valore assoluto, ma segno negativo, mentre il cateto OH decresce verso 0 in valore assoluto ed il suo segno rimane negativo.
Quindi se

PH = -1
OH = 0

Continuando a far crescere l’angolo

, il valore di PH da -1 torna verso lo zero, mentre il cateto OH, da zero aumenta verso 1.
Se

si ha che

poiche PH = 0

poiché OH = 1.
Da questo momento in poi il punto P ricomincia il giro sulla circonferenza ripartendo dall’origine degli archi, per cui sia il seno sia il coseno riassumono gli stessi valori descritti sopra.
In base a queste considerazioni si arriva alle seguenti conclusioni:

• seno e coseno hanno valori compresi fra -1 e 1;
• la funzione tangente valori compresi fra -infinito a +infinito;
• seno e coseno sono funzioni periodiche di periodo 2\pi;
• il segno delle funzioni seno e coseno varia nel seguente modo
  primo quadrante: seno positivo e coseno positivo;
  secondo quadrante: seno positivo e coseno negativo;
  terzo quadrante: seno e coseno negativi;
  quarto quadrante: seno negativo e coseno positivo
.

Il grafico delle funzioni seno e coseno può essere ricavato dai valori che tali funzioni assumono in base al valore dell’angolo

:
sinusoide è il nome attribuito al grafico del seno, cosinusoide quello il grafico del coseno.

Relazione fondamentale

Le funzioni seno e coseno sono legate dalla relazione fondamentale:

La dimostrazione di tale relazione viene fatta tramite il Teorema di Pitagora:

ma

per il Teorema di Pitagora
quindi

da cui la nostra tesi.

Angoli e lati di un triangolo

La trigonometria, come già anticipato, mette in relazione i lati di un triangolo con i suoi angoli:
I principali teoremi che ci forniscono queste relazioni sono:

• il teorema dei triangoli rettangoli;
• il teorema dei seni;
• il teorema di Carnot o dei coseni.

Questi due ultimi teoremi sono validi per qualunque triangolo.
Il teorema dei triangoli rettangoli asserisce che:
dato un triangolo rettangolo ABC, in cui
BC è l’ipotenusa
l’angolo in A è

è l’angolo in C

è l’angolo in B,
si ha che

Il teorema dei seni afferma che:
dato un triangolo qualunque ABC in cui

è l’angolo in A

è l’angolo in B

è l’angolo in C
Il rapporto fra un lato ed il seno dell’angolo opposto è costante e più precisamente

dove R è il raggio della circonferenza circoscritta al triangolo ABC.
Il teorema di coseni o di Carnot asserisce che, dato un triangolo qualunque come sopra, il quadrato di un lato è uguale alla somma dei quadrati degli altri due meno il doppio prodotto fra gli altri due lati ed il coseno dell’angolo compreso fra questi.

per ulteriori approfondimenti sulla trigonometria vedi anche qua