Inversione rispetto al cerchio – Definizione e formule

In questo appunto viene approfondita l’inversione rispetto al cerchio, viene fornita una definizione, vengono descritte le formule che descrivono tale trasformazione, vengono descritte le proprietà caratteristiche dell’inversione e la composizione di due inversioni.

Inversione rispetto al cerchio

L'inversione rispetto al cerchio è un tipo di trasformazione che non rientra nella tipologia di trasformazioni delle affinità. Ricordiamo che una trasformazione affine è una corrispondenza biunivoca tra piani o punti appartenenti allo stesso piano, che trasforma le rette in rette e che mantiene il parallelismo tra esse; esempi di trasformazioni affini sono la rotazione, la traslazione e le riflessioni. Definizione: Dato un cerchio (

[math]\gamma[/math]

) di centro O e raggio r, si dice inversione di centro O e potenza

[math]r^2[/math]

la trasformazione che associa ad ogni punto P del piano il punto P' della semiretta OP tale che: In particolare, il numero viene definito potenza dell'inversione, mentre la circonferenza () si dice cerchio di inversione. Conoscendo la posizione del punto P è possibile ricostruire geometricamente la posizione del punto P'; vediamo alcuni casi:

• P è esterno alla circonferenza (
  [math]\gamma[/math]
  ): In questo caso, si traccia la circonferenza di diametro OP; consideriamo il punto M, uno dei punti di intersezione con (
  [math]\gamma[/math]
  ); il punto P' è la proiezione ortogonale di M su OP.
• P è interno alla circonferenza (
  [math]\gamma[/math]
  ): Si conduce da P la perpendicolare alla retta OP e si indicano con N ed M i punti in cui questa incontra la circonferenza (
  [math]\gamma[/math]
  ); P' è il punto di intersezione delle tangenti a (
  [math]\gamma[/math]
  ) condotte da N e M.
• P è un punto della circonferenza (
  [math]\gamma[/math]
  ): In questo caso, P' coincide con P; infatti, ad ogni punto P corrisponde uno e un solo punto P' e viceversa, e tutti i punti di (
  [math]\gamma[/math]
  ) sono punti uniti, vengono cioè mandati in se stessi dalla trasformazione.

La trasformazione inversa dell'inversione rispetto al cerchio è l'inversione stessa; ciò significa che, componendo un'inversione con se stessa, otteniamo l'identità. L’identità è quella trasformazione che applicata ad un elemento ci fornisce l’elemento stesso. Per ulteriori approfondimenti sull'affinità e le trasformazioni vedi anche qua

Formule dell'inversione

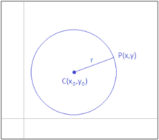
Consideriamo l'origine O del sistema di riferimento cartesiano come il centro della circonferenza di inversione, e prendiamo un punto P, di coordinate ( x ; y ), e un punto P', di coordinate ( x' ; y' ), corrispondenti nell'inversione di centro O e potenza . Ricordiamo che la circonferenza è il luogo geometrico dei punti caratterizzati dall’avere la stessa distanza da un punto particolare che prende il nome di centro; l’equazione della circonferenza non è altro che la trascrizione in formula della definizione di circonferenza. Ricordiamo che l’equazione generica di una circonferenza con centro nell’origine degli assi e raggio r è: Considerando la trasformazione rispetto al cerchio abbiamo quindi che: Ricordando le formule delle equazioni delle circonferenza di centro O e diametro OP e OP': e sostituendole nella relazione precedente, otteniamo delle formule che descrivono la trasformazione, e ci permettono di determinare le coordinate del punto P' conoscendo quelle del punto P: Da questa relazione, possiamo ricavare le formule della trasformazione inversa, che ci permettono di determinare le coordinate del punto P conoscendo quelle del punto P':

Proprietà caratteristica dell'inversione

Una delle principali proprietà dell'inversione rispetto al cerchio è che due punti qualunque e i loro inversi si trovano su una stessa circonferenza, oppure sono allineai con il centro dell'inversione. Per quanto riguarda la composizione di inversioni aventi lo stesso centrosi ha che: il prodotto, o composizione, di due inversioni aventi lo stesso centro O, e potenza diversa, è un'omotetia di centro O. In particolare, due figure inverse di una stessa figura, rispetto allo stesso centro O, si corrispondono in una omotetia di centro O.

Figure inverse di alcuni elementi geometrici

Vediamo cosa accade nel caso in cui sia trasformata un'intera retta con una inversione rispetto al cerchio.

• Ogni retta passante per il centro della circonferenza d'inversione viene trasformata in se stessa; infatti, punti corrispondenti sono allineati con il centro O;
• Ogni retta non passante per il centro della circonferenza d'inversione viene trasformata in una circonferenza passante per O.

Consideriamo il caso in cui questo tipo di trasformazione sia applicato ad una circonferenza.

• Ad ogni circonferenza C passante per il centro O della circonferenza d'inversione corrisponde una retta non passante per O;
• Ad ogni circonferenza C non passante per il centro O della circonferenza di inversione corrisponde una circonferenza C' non passante per O.

Per ulteriori approfondimenti sulla circonferenza e sulla sua equazione vedi anche qua