Circonferenza e cerchio: definizione e formulario

Nei seguenti paragrafi verrà approfondito e definito il concetto di circonferenza, descrivendone nel dettaglio i suoi elementi principali; con approfondimenti relativi ai suoi elementi. Vedremo anche, di conseguenza, le formule utili a calcolare determinati elementi che fanno parte di una circonferenza.

Definizione di circonferenza

La circonferenza è un "luogo geometrico", che in geometria indica semplicemente un insieme di punti che hanno la stessa proprietà; nel nostro caso, la proprietà in questione è correlata ad una distanza da un punto fisso.
Per essere più precisi, diamo la seguente definizione:la circonferenza è l'insieme di tutti i punti che hanno la stessa distanza da un punto fissato detto centro.
Tale distanza si chiama raggio ed è la metà del diametro, ossia il segmento più lungo che puoi tracciare all'interno di un cerchio e va da una parte all'altra della circonferenza passando per il centro.

Corde e diametri

Abbiamo definito la circonferenza nel paragrafo precedente: ossia un insieme di punti che soddisfano una certa proprietà.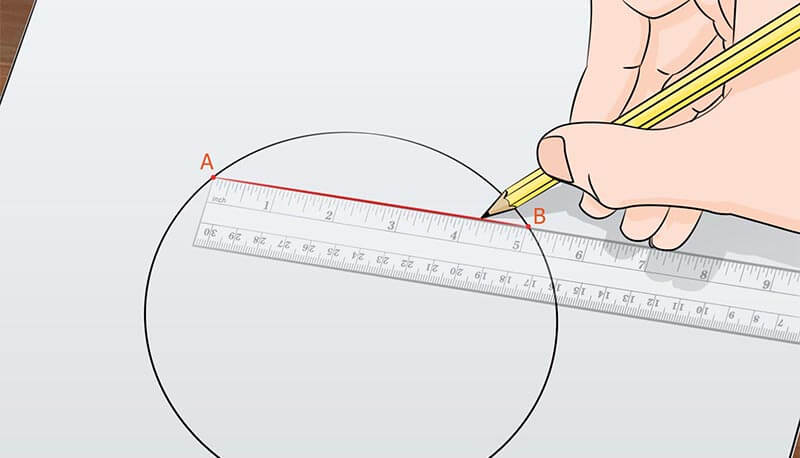 Presi due punti distinti qualsiasi, appartenenti alla circonferenza, diremo corda un qualsiasi segmento che congiunge due punti qualsiasi della circonferenza in questione. Le corde possono essere infinite, ma c'è una corda particolare: il diametro, come abbiamo accennato nel paragrafo precedente, è la corda massima della circonferenza ed è pari al doppio della lunghezza del raggio. Non esiste quindi corda più lunga del diametro; se esistesse, avrebbe almeno un vertice fuori dalla circonferenza, contraddicendo la definizione di corda.

Cerchio

Bisogna fare molta attenzione a distinguere bene il cerchio dalla circonferenza. Sebbene la denominazione simile possa trarre in inganno, i due concetti sono ben diversi. La circonferenza è stata infatti definita all'inizio, il cerchio lo definiamo invece come la parte di piano racchiusa (o delimitata) dalla circonferenza.
Potremmo quindi dire, sfruttando entrambe le definizioni, che il cerchio è una figura, dotata di una certa area, mentre la circonferenza rappresenta il perimetro del cerchio.

Calcolo della circonferenza

A partire dalla definizione, il valore della circonferenza, che rappresenta il perimetro del cerchio, si può trovare utilizzando il raggio tramite la formula:
Tuttavia, possiamo ricordare che abbiamo definito il diametro come la corda massima con misura doppia rispetto al raggio. Chiamiamo quindi il diametro, potremo dire che . Di conseguenza, la circonferenza può essere calcolata anche con la formula:
Da quest'ultima formula possiamo ricavare le formule inverse, ad esempio, è possibile ricavare il diametro a partire dalla circonferenza con la formula:
Una volta ottenuta la misura del diametro, si può risalire alla misura del raggio semplicemente dividendo per 2.
Per approfondimenti sul calcolo della circonferenza, vedi anche qua.

Area del cerchio

L'area del cerchio (e non della circonferenza, la circonferenza è una linea chiusa che ha quindi area nulla!) si calcola con la seguente formula:
Ricordando che , possiamo scrivere la formula sopra come:
Dalle formule scritte sopra, possiamo ricavare anche le relative formule inverse:
Siccome , una volta ottenuto il raggio è possibile passare facilmente alla misura del diametro.

Dal cerchio alla circonferenza, e viceversa

Viste le formule ricavate nel paragrafo precedente, possiamo trovare anche una formula per passare dal valore dell'area al valore della circonferenza.
La formula è , ottenuta sostituendo il valore di ricavato prima.
Di conseguenza sarà possibile anche passare dalla circonferenza all'area, con la formula inversa:

Esercizio di esempio

Considerata una circonferenza di raggio , calcoliamone la sua misura e l'area del cerchio racchiuso in essa.
Usiamo le formule opportune, calcolando dapprima:

• Misura della circonferenza: applichiamo la formula:
  [math] C = 2 \pi r = 2 \pi \cdot 8 \text{cm} = 16 \pi \text{cm} = 50.24 \text{cm} [/math]
• Area del cerchio: applichiamo la formula:
  [math] C = r^2 \pi = (8 \text{cm})^2 \pi = 64 \pi \text{cm}^2 = 200.96 \text{cm}^2 [/math]

In sintesi, la circonferenza misura circa 50,24 mentre l'area del cerchio vale circa 200,96 .
Nota: è un numero irrazionale. Negli esercizi puoi lasciarlo così oppure inserirlo nel conto approssimandolo con 3,14.
Per approfondimenti sul pi greco, vedi anche qua.