Iperbole - Conica non degenere: proprietà ed equazione

Nell’appunto è descritta l’iperbole, conica non degenere come parabola ed ellisse. Partendo dalla definizione come luogo geometrico di punti, si passa ai suoi elementi caratteristici, fuochi, vertici, asintoti. Viene inoltre data l’equazione canonica sia quando i fuochi dell’iperbole sono sull’asse x che quando sono sull’asse y. Segue la definizione dell’eccentricità e il suo significato ed infine un cenno alle superfici iperboliche.

Iperbole - Conica non degenere

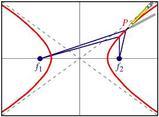
L'iperbole è il luogo geometrico dei punti P del piano per i quali è costante il valore assoluto della differenza delle distanze da due punti fissi, detti fuochi.
In altre parole, presi due punti

che appartengono all'iperbole, detti

e

i due fuochi, detto k il valore della differenza delle distanze, si ha:

il valore assoluto si rende necessario perché a seconda del ramo cui appartiene il punto, la differenza tra le due distanze può essere anche negativa

L'iperbole, assieme alla circonferenze, l'ellisse e la parabola, fa parte delle curve che vengono chiamate "coniche non degeneri", sono un'intersezione tra un piano e un cono a due falde e il polinomio che ne rappresenta l’equazione è irriducibile nel campo dei numeri complessi.

Detto

l'angolo tra l'asse del cono e la sua retta generatrice (guarda la figura sovrastante), se prendiamo un piano

inclinato di un angolo

rispetto all’asse e minore di

, la sua intersezione con il cono a due falde da origine all'iperbole.

Poiché il piano interseca entrambe le falde, l'iperbole è formata da due curve separate che costituiscono i due rami distinti dell'iperbole.

Elementi dell’iperbole

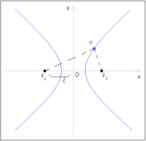
Come per le altre coniche, l’equazione è diversa a seconda della posizione rispetto al sistema di riferimento. Nel piano cartesiano, consideriamo ora un’iperbole con il centro nell’origine degli assi e con i fuochi sull’asse x. L’iperbole è una curva simmetrica rispetto all’asse delle ascisse, rispetto all’asse delle ordinate e anche rispetto all’origine.
Quella che vedi in figura è di questo tipo. Quando i fuochi sono sull’asse y, i due rami intersecano l’asse delle ordinate. I punti di intersezione sono i vertici indicati con (

). La distanza tra i vertici è detta asse trasverso e la sua misura è 2a. L’iperbole essendo costituita da due rami distinti non è una curva chiusa. Man mano che ci si allontana dall’origine, entrambi i rami si avvicinano sempre più a due rette, dette asintoti che in figura sono le rette passanti per l’origine sulle quali si trovano anche le diagonali del rettangolo di lati 2a e 2b. Asintoto deriva dal greco e significa appunto «che non incontra».
La distanza 2b è anche la misura dell’asse non trasverso, definito come la distanza tra i due vertici non reali indicati in genere con

.

Equazione in forma canonica

Quando i fuochi

sono disposti sull’asse x, oppure sull’asse

, in modo che l’origine O sia il punto medio del segmento

, l’equazione dell’iperbole si presenta in una forma semplice, che è detta equazione canonica (o normale). L'equazione dell'iperbole, in forma canonica con i fuochi sull’asse

è la seguente:

In virtù delle simmetrie della curva, l’equazione di un’iperbole è riferita quindi al suo centro e ai suoi assi di simmetria, o, come più semplicemente si dice, equazione di un’iperbole riferita al centro e agli assi. Somiglia a quella dell’ellisse tranne per il segno meno che compare al primo membro, questo aiuta a ricordarla. L’equazione contiene due parametri che sono le misure dei semiassi, legati a loro volta al terzo parametro c, che è la semidistanza focale. La relazione tra questi parametri è la seguente:

Le coordinate dei vertici e dei fuochi sono rispettivamente:

mentre gli asintoti hanno equazione:

Gli asintoti dunque non hanno punti in comune con l’iperbole e sono di fondamentale importanza per disegnare l’iperbole di equazione canonica assegnata. Si dimostra anche che i due rami che costituiscono l’iperbole sono contenuti internamente alla coppia di angoli opposti al vertice che sono determinati dai due asintoti e che contengono i fuochi e i vertici della curva.
Quando a=b l'iperbole viene detta equilatera

Iperbole con i fuochi sull’asse y

Quando i fuochi sono sull’asse delle ordinate, per la simmetria fuochi e vertici reali hanno le seguenti coordinate:

la distanza focale è:

con

l’equazione assume la forma seguente:

tra i parametri vale allora la relazione:

le equazioni degli asintoti restano invariate

Eccentricità-significato

L'eccentricità di un’iperbole è il rapporto tra la distanza focale e lunghezza dell’asse trasverso. Per un’iperbole con i fuochi sull’asse x abbiamo:

ricordando la formula della semidistanza focale possiamo scrivere anche:

Per un’iperbole con i fuochi sull’asse y abbiamo:

ricordando la formula della semidistanza focale:

Dato che in una qualsiasi iperbole la distanza focale è maggiore della misura dell’asse trasverso, si ha sempre

.
L’eccentricità di un’iperbole misura l’«apertura» dei suoi rami. Tenendo costante l’asse trasverso, all’aumentare dell’eccentricità i fuochi si allontanano dai vertici e i rami sono sempre più aperti.

Edifici iperbolici

Esistono edifici la cui superficie è un iperboloide, una superficie ottenuta dalla rotazione di un’iperbole intorno al suo asse non trasverso. Per ogni punto di questa superficie passano sempre due rette che appartengono completamente alla superficie stessa.
Nell'ingegneria questa forma costruttiva ha due vantaggi importanti:

In termini di sicurezza offre il minimo profilo al vento e quindi basso rischio di essere abbattuta da venti di eccezionale intensità. Un esempio è la Tornado Tower, situata in Qatar, che ha un profilo iperbolico ed è alta 195 metri.

Per approfondimenti sull'iperbole e la geometria analitica