In questo appunto di matematica si tratta un particolare tipo di curva, l’iperbole equilatera, definendone equazione e caratteristiche e la funzione omografica.
Indice
L’iperbole
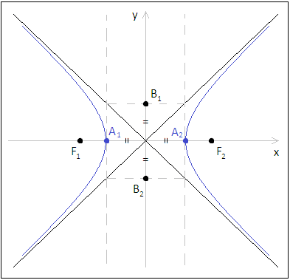
Si definisce iperbole il luogo geometrico dei punti del piano per cui è costante la differenza delle distanze da due punti fissi,
F_1
[/math]
ed
F_2
[/math]
, detti fuochi.
Supposto che tali punti si trovino sull’asse delle ascisse, x, avremo che:
F_1 = (-c;0)
[/math]
F_2 = (+c;0)
[/math]
ossia
F_1F_2 = 2c
[/math]
chiamata distanza focale.
Considerato il punto generico P = (x;y) del piano cartesiano, per definizione si ha che
PF_1 – PF_2 = 2a
[/math]
dove a è una costante.
Dalla precedente espressione, con opportuni calcoli ed imponendo
c^2 - a^2 = b^2
[/math]
si ottiene l’equazione canonica o normale dell’iperbole avente i fuochi sull’asse x:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1.
[/math]
Il valore di a prende il nome di semiasse trasverso (quindi 2a viene detto asse trasverso),
ed i punti
A_1 = (-a;0)
[/math]
e
A_2 = (a;0)
[/math]
sono chiamati vertici dell’iperbole.
Il valore di b viene chiamato semiasse non trasverso (2b è l’asse non trasverso).
In modo del tutto analogo, se i fuochi si trovano sull’asse delle ordinate, y, avremo che:
F_1 = (0;-c)
[/math]
F_2 = (0;+c)
[/math]
|PF_1 – PF_2| = 2b
[/math]
avendo indicato con b la costante.
Tramite opportuni calcoli ed imponendo
c^2 – b^2 = a^2
[/math]
otteniamo l’analoga equazione canonica dell’iperbole con i fuochi sull’asse y:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1.
[/math]
Dall’equazione dell’iperbole si deducono alcune sue proprietà.
L’iperbole è simmetrica rispetto agli assi coordinati che si definiscono assi dell’iperbole.
L’iperbole è simmetrica rispetto all’origine degli assi che viene chiamata centro dell’iperbole.
L’iperbole equilatera
Si chiama iperbole equilatera una qualsiasi iperbole i cui semiassi trasverso e non trasverso hanno la stessa misura: a = b.
Consideriamo un'iperbole equilatera riferita ai propri assi, avente per esempio i fuochi appartenenti all’asse delle ascisse:
F_1 = (-c; 0)
[/math]
F_2 = (+c; 0)
[/math]
Visto che in questo caso in virtù della definizione a = b, la sua equazione sarà
\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1
[/math]
ossia
x^2 - y^2= a^2.
[/math]
Dal momento che la semidistanza focale si calcola come
c = \sqrt{a^2 + b^2}
[/math]
in questo caso risulta
c = \sqrt{2a^2} = a \sqrt{2}
[/math]
indipendentemente dal fatto che i vertici siano disposti orizzontalmente o verticalmente.
L’eccentricità dell’iperbole equilatera, in base a quanto scritto sopra, è la seguente:
e = c/a = \sqrt{2}.
[/math]
Le equazioni degli asintoti degli asintoti dell’iperbole equilatera si ricavano dalle equazioni di una iperbole generica:
y = \pm (\frac{b}{a})x,
[/math]
nel caso dell’iperbole equilatera abbiamo
y = \pm x
[/math]
poiché a = b.
Gli asintoti coincidono dunque con le bisettrici dei quadranti, e sono per questo tra loro ortogonali.
Nel caso in cui l'iperbole equilatera sia traslata, risulteranno traslati anche gli asintoti e quindi la loro perpendicolarità sarà mantenuta.
Iperbole equilatera riferita ai propri asintoti
In base a quanto asserito precedentemente, gli asintoti di un'iperbole equilatera sono ortogonali, proprio come gli assi coordinati.
Viene allora naturale domandarsi come si modificherebbe l'equazione dell'iperbole qualora, operando una rotazione di 45° in senso orario o antiorario, si portassero gli asintoti dell'iperbole a coincidere con gli assi cartesiani x ed y.
In base al fatto che l'iperbole è equilatera, la distanza focale è data da
2c = 2a \sqrt{2}
[/math]
ciò significa che ciascuno dei fuochi, che adesso si vengono a trovare su una delle bisettrici dei quadranti (ad esempio su quella del primo e del terzo), disterà dall'origine
c = a \sqrt{2}.
[/math]
I fuochi avranno dunque coordinate
F_1 = (-a, a)
[/math]
F_2= (a, a).
[/math]
Possiamo ora procedere come al solito in base alla definizione per ricavare l'equazione dell’iperbole:
|PF_1 - PF_2| = 2a
[/math]
elevando al quadrato si ottiene che:
(PF_1 - PF_2)^2 = 4 a^2
[/math]
\big(\sqrt{(x+a)^2+(y+a)^2} - \sqrt{(x-a)^2 + (y-a)^2}\big)^2 = 4 a^2
[/math]
Svolgendo i calcoli otteniamo la seguente espressione
[x^2 + a^2 + 2ax + y^2 + a^2 + 2ay + x^2 + a^2 - 2ax + y^2 + a^2 - 2ay - 4a^2 ] =
[/math]
= [2 \sqrt{[(x+a)^2 + (y+a)^2][(x-a)^2 + (y-a)^2]}]
[/math]
ossia
[2x^2 + 2y^2 = 2\sqrt{[(x+a)^2 + (y+a)^2][(x-a)^2 + (y-a)^2]}]
[/math]
Da cui, dividendo per due entrambi i membri ed elevando nuovamente al quadrato per eliminare la radice quadrata, si ha che:
[(x^2 + y^2)^2 = [(x^2 + 2a^2 + y^2) + (2ax + 2ay)][(x^2 + 2a^2 + y^2) - (2ax + 2ay)]]
[/math]
[x^4 + y^4 + 2(x^2)(y^2) = (x^2 + 2a^2 + y^2)^2 - (2ax + 2ay)^2]
[/math]
[x^4 + y^4 + 2(x^2)(y^2) = x^4 + 4a^4 + y^4 + 4(a^2)(x^2) + 4(a^2)(y^2) + 2(x^2)(y^2) – 4(a^2)(x^2) – 4(a^2)(y^2) – 8(a^2)(xy)]
[/math]
8a^2xy=4a^4
[/math]
xy = \frac{a^2}{2}
[/math]
ossia concludiamo
xy = k.
[/math]
L'ultima equazione essendo stata ottenuta indicando con k il numero positivo
\frac{a^2}{2}.
[/math]
L'equazione ottenuta, xy = k, è quella ricercata dell'iperbole equilatera riferita ai propri asintoti.
Si noti che qualora avessimo scelto di posizionare i fuochi sull'altra bisettrice dei quadranti (bisettrice del secondo e del quarto quadrante), ovvero se avessimo effettuato una rotazione di 45° nel senso opposto, avremmo ottenuto la medesima equazione, ma con
k = - \frac{a^2}{2}.
[/math]
Come si vede dai grafici riportati, l'iperbole equilatera riferita ai propri asintoti è una funzione monotona definita su tutto l’insieme dei numeri reali escluso il punto x = 0.
Funzione omografica
Considerata un iperbole equilatera che ha gli asintoti paralleli agli assi cartesiani, definiamo funzione omografica una funzione di equazione:
y = \frac{ax + b}{cx + d}
[/math]
nella quale i coefficienti a, b, c e d sono numeri reali, in cui c deve essere diverso da zero, poiché in caso contrario l’espressione dell’omografica si ridurrebbe all’equazione di una semplice retta.
Tale funzione ha asintoto verticale
x = -\frac{d}{c}
[/math]
ed asintoto orizzontale
y = \frac{a}{c}.
[/math]
Le coordinate del centro di simmetria sono:
C = \big(-\frac{d}{c}; \frac{a}{c}\big).
[/math]
Vogliamo adesso mostrare che una funzione omografica consiste in un'iperbole equilatera riferita ai propri asintoti traslata in modo tale che il suo centro sia il punto
O'\big(-\frac{d}{c}, \frac{a}{c}\big)
[/math]
Precedentemente indicato con C, centro di simmetria.
Per fare ciò ci limiteremo a prendere l'equazione della funzione omografica come da definizione ed a traslarla in direzione inversa, mostrando che otteniamo così un'equazione del tipo
XY=k.
[/math]
Siano
X = x + \frac{d}{c}
[/math]
Y = y - \frac{a}{c}
[/math]
Sostituendo i valori di X ed y nell’espressione della funzione omografica, otteniamo:
Y + \frac{a}{c} = \frac{a \big(X - \frac{d}{c}\big) + b}{c\big(X - \frac{d}{c}\big) + d}
[/math]
e dunque, svolgendo i calcoli,
Y = \frac{aX - \frac{ad}{c} + b}{cX – d + d} - \frac{a}{c}
[/math]
da cui otteniamo
Y = \frac{aX - \frac{ad}{c} + b}{cX} - \frac{a}{c}
[/math]
quindi
Y = \frac{aX - \frac{ad}{c} + b - aX}{cX}
[/math]
da cui,
Y = \frac{-\frac{ad}{c} + b}{cX}
[/math]
ed infine
XY = -\frac{ad}{c^2} + \frac{b}{c}
[/math]
XY=k
[/math]
avendo imposto
k = -\frac{ad}{c^2} + \frac{b}{c}.
[/math]
Tale valore di k, grazie alle limitazioni richieste per i parametri a, b, c e d (c diverso da zero), è sensato e non nullo, dunque l'equazione ottenuta è proprio quella di un'iperbole equilatera riferita ai propri asintoti.
Come si può vedere dal grafico e dai calcoli, la funzione omografica è dunque un'iperbole equilatera riferita ai propri asintoti il cui centro di simmetria è stato traslato da O = (0, 0) nel punto
(O'\big(-\frac{d}{c}, \frac{a}{c}\big)).
[/math]
Come tale iperbole, anch'essa è una funzione, dal momento però che i suoi asintoti sono le rette
x = -\frac{d}{c}
[/math]
e
y = \frac{a}{c}
[/math]
la funzione omografica è definita ovunque tranne che in
x = -\frac{d}{c}
[/math]
ed assume tutti i valori reali tranne
y = \frac{a}{c}.
[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
