In questo appunto di matematica tratteremo una particolare curva, l’ellisse e la sua equazione e come arrivare a tale equazione noti alcuni dati.
Indice
Definizione di ellisse
Chiameremo ellisse il luogo geometrico dei punti del piano per i quali è costante la somma delle distanze da due punti fissi, detti fuochi.
Quindi considerato un generico punto P = (x;y) e chiamati
F_1
[/math]
ed
F_2
[/math]
i fuochi si ha che:
PF_1 + PF_2 = 2a
[/math]
dove
F_1F_2 = 2c
[/math]
è la distanza fra i due fuochi
mentre 2a è la somma costante anzidetta.
Si ricordi che a>c perché in un triangolo la somma di due lati è maggiore del terzo.
Infatti affinché tale luogo geometrico esista, è necessario che la costante che indica la somma delle distanze dai fuochi
F_1
[/math]
ed
F_2
[/math]
di un punto P = (x;y) appartenente all'ellisse, sia maggiore della lunghezza del segmento
F_1F_2
[/math]
, detta distanza focale.
Infatti, qualunque sia il punto del piano P = (x;y), per la disuguaglianza triangolare deve risultare:
PF_1 + PF_2 > F_1F_2.
[/math]
La definizione data per l’ellisse non esclude l'eventualità che i fuochi siano coincidenti.
In tal caso l'osservazione fatta sulla condizione di esistenza del luogo geometrico è superflua, poiché qualunque numero reale positivo si scelga come costante per la somma, esso risulterà certamente maggiore di
F_1F_2 = 0
[/math]
.
In questo caso il luogo geometrico si riduce ad una circonferenza, visto che esso è composto da quei punti tali che il doppio della distanza da un punto fisso sia costante; è facile verificare questa tesi anche adoperando il metodo di costruzione dell’ ellisse sposto di seguito.
Ne risulta che la circonferenza non è che una particolare ellisse.
Ellisse del giardiniere
Esiste un modo semplice per costruire fisicamente un'ellisse. Tale metodo ha anche il pregio di illustrare chiaramente in maniera visiva il significato della definizione data precedentemente.
Si immagini di fissare sul terreno due punti
F_1
[/math]
ed
F_2
[/math]
, per esempio utilizzando dei paletti, e di legare le due estremità di una fune a detti punti; la lunghezza della fune deve risultare maggiore rispetto alla distanza tra
F_1
[/math]
ed
F_2
[/math]
.
Con un terzo paletto (che rappresenta il punto P precedentemente definito) si tenda adesso la corda: si nota che il punto P non è fisso, ma può essere spostato in varie posizioni avendo sempre cura di tenere la fune tesa. Se si fa in modo che il punto P occupi tutte le posizioni possibili, esso traccerà sul terreno una linea curva che racchiude i punti
F_1
[/math]
ed
F_2
[/math]
: la curva geometrica ottenuta è un’ellisse.
Infatti comunque si prenda un punto appartenente a detta curva è chiaro che la somma delle sue distanze da
F_1
[/math]
ed
F_2
[/math]
è sempre uguale alla lunghezza della fune, quindi costante per ogni punto.
Tale costruzione è denominata "ellisse del giardiniere" poiché essa consente, con mezzi di fortuna, di tracciare nel terreno aiuole di forma perfettamente ellittica.
Equazione dell'ellisse riferita ai propri assi
Si vuole determinare l’equazione cartesiana dell’ellisse, ossia un’equazione in due variabili che risulti soddisfatta dalle coordinate di tutti e soli i punti della curva considerata.
Considerato un sistema di riferimento cartesiano ortogonale, si fissino i fuochi
F_1
[/math]
ed
F_2
[/math]
sull’asse delle x e assumiamo l’asse y passante per il punto medio del segmento
F_1F_2
[/math]
, punto in cui fisseremo l’origine O del sistema di riferimento. In tale caso avremo che le coordinate dei fuochi sono espresse da:
F_1 = (-c;0)
[/math]
F_2 = (c;0).
[/math]
Affinché il punto P = (x;y) appartenga all’ellisse deve soddisfare la condizione
PF_1 + PF_2 = 2a
[/math]
In base alla definizione di distanza fra due punti si ha che:
PF_1 = \sqrt[2]{(x + c)^2 + y^2}
[/math]
PF_2 = \sqrt[2]{(x - c)^2 + y^2}
[/math]
per cui si ottiene
\sqrt[2]{(x + c)^2 + y^2} + \sqrt[2]{(x - c)^2 + y^2} = 2a
[/math]
\sqrt[2]{(x - c)^2 + y^2} = 2a - \sqrt[2]{(x + c)^2 + y^2}
[/math]
Elevando entrambi i membri al quadrato
(x - c)^2 + y^2 = 4a^2 + (x + c)^2 + y^2 – 4a \sqrt[2]{(x + c)^2 + y^2}
[/math]
4a \sqrt[2]{(x + c)^2 + y^2} = -(x - c)^2 + 4a^2 + (x + c)^2
[/math]
a \sqrt[2]{(x + c)^2 + y^2} = a^2 + cx
[/math]
elevando ancora al quadrato
(a^2 – c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)
[/math]
posto per brevità
a^2 – c^2 = b^2
[/math]
dove b è un numero reale positivo in quanto a>c si ottiene
b^2x^2 + a^2y^2 = a^2b^2
[/math]
da cui si ottiene la forma generale
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
[/math]
la precedente viene chiamata equazione canonica o normale dell’ellisse.
Proprietà dell’ellisse
Una prima proprietà dell’ellisse è che il suo grafico è simmetrico rispetto agli assi coordinati.
L’equazione canonica dell’ellisse contiene solo potenze pari della x e della y, conseguentemente se la coppia
(x_1,y_1)
[/math]
la soddisfa, sarà soddisfatta anche dalla coppia
(x_1, -y_1)
[/math]
:
se il punto
P = (x_1,y_1)
[/math]
appartiene all’ellisse lo stesso vale per il punto
Q = (x_1, -y_1)
[/math]
che è il simmetrico di P rispetto all’asse delle ascisse. Per lo stesso motivo è simmetrica anche rispetto all’asse delle ordinate.
Per tale motivo i due assi coordinati sono chiamati assi dell’ellisse.
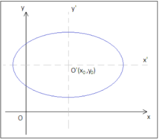
Conseguentemente alla simmetria dell’ellisse rispetto agli assi ne deriva che è simmetrica rispetto all’origine degli assi che sono fra loro perpendicolari e l’origine del sistema di riferimento viene chiamato centro dell’ellisse.
L’ellisse è inscritta in un rettangolo definito dalle rette di equazioni x = ± a ed y = ± b, da cui deriva che
-a \le x \le a
[/math]
-b \le x \le b.
[/math]
I punti di intersezione dell’ellisse con gli assi coordinati sono
(± a; 0) intersezione con l’asse x
(0; ± b) intersezione con l’asse y
tali punti vengono chiamati vertici.
La distanza fra i punti di intersezione dell’ellisse con l’asse x, pari a 2a, viene definito asse maggiore, mentre la distanza fra i punti di intersezione dell’ellisse con l’asse y, pari a 2b, viene definito asse minore.
Conseguentemente a viene chiamato semiasse maggiore e b semiasse minore; i fuochi si trovano sempre sull’asse maggiore che viene anche chiamato asse focale.
Una grandezza che caratterizza l’ellisse è l’eccentricità, definita come:
e = \frac{c}{a}
[/math]
dove
0 \le e \le 1
[/math]
se e = 0 l’ellisse è una circonferenza.
L’eccentricità è una misura di quanto l’ellisse per la sua forma più o meno allungata, differisce dalla circonferenza.
Come si ricava l’equazione dell’ellisse
L’equazione dell’ellisse
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
[/math]
dipende dai parametri a e b, quindi per determinare l’equazione di una particolare ellisse servono due condizioni tali che ci permettano di impostare un sistema di due equazioni in due incognite le cui soluzioni sono tali parametri.
Escluso il caso in cui sono note le lunghezze dell’asse maggiore e di quello minore, si possono avere i seguenti casi:
- equazione dell’ellisse noti due suoi punti;
- equazione dell’ellisse noto un suo punto ed uno dei due fuochi;
- equazione dell’ellisse noto uno dei due fuochi e la sua eccentricità;
- equazione dell’ellisse noto un suo punto e la sua eccentricità.
Dalle condizioni precedentemente elencate ne possono conseguire altre.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
