In questo appunto verrà descritto appieno il concetto di iperbole descritto come luogo geometrico nel piano cartesiano, attraverso le sue proprietà e formule principali.
Indice
Definizione di iperbole
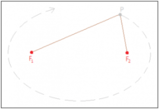
In matematica è necessario andare a definire l'iperbole come un luogo geometrico, qui di seguito la definizione formale.
Si chiama iperbole il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi distinti, detti fuochi.
Osservazione 1
Da qui è necessario andare ad effettuare alcune osservazioni importanti.
Perché il luogo geometrico sia non vuoto, è necessario che la costante che indica la differenza delle distanze dai fuochi
ed
di un punto P appartenente all'iperbole sia minore della lunghezza del segmento
, detta distanza focale. Infatti, qualunque sia il punto appartenente al piano, per la disuguaglianza triangolare deve risultare sempre la seguente relazione valida per l'iperbole riportata così come segue:
nella quale l'uguaglianza vale solo nel caso in cui i tre punti sono allineati.
Osservazione 2
Un'altra osservazione importante da effettuare è che la differenza tra le lunghezze dei due segmenti
e
perché, a priori, non sappiamo quale dei due segmenti è più lungo. Ogni iperbole è infatti composta sia di punti P tali che
sia di punti che risultino tali che
Osservazione 3
La definizione di iperbole così formulata va ad escludere sin dal principio l'eventualità che i fuochi siano coincidenti. In quel caso infatti dovendosi sempre avere la relazione così come segue:
Da cui è possibile osservare che risulterà anche che:
Da ciò, si può andare a concludere che avremmo che l'iperbole sarebbe costituita da tutti e soli quei punti tali che deve risultare:
Dal momento però che i fuochi sono coincidenti, questa relazione è verificata da tutti i punti del piano: ne risulta che il luogo geometrico non rappresenta più ciò che ci eravamo preposti di definire.
Equazione dell'iperbole riferita ai propri assi
Metodo per ricavare l'equazione: Per trovare l'equazione dell'iperbole mettiamoci in primo luogo nel caso semplice in cui i fuochi sono posti sull'asse x e sono equidistanti dall'origine. Se allora diciamo
, le coordinate dei fuochi saranno i seguenti riportati:
Detto adesso che un qualsiasi punto del piano di coordinate cartesiano, e fissato un numero tale per cui risulti sempre che:
Si può concludere che per la definizione dell'iperbole apparterrà all'iperbole quel punto se e solo se risulterà che:
Elevando tutto al quadrato, il valore assoluto scompare è otteniamo dunque queste relazioni susseguite da differenti passaggi matematici:
Si procede ora andando a isolare la radice ed elevando nuovamente al quadrato, avremo poi i seguenti passaggi matematici che ci porteranno alla soluzione finale:
Dalla quale, semplificando si otterrà il risultato finale come segue:
Ricordando infine che deve valere la seguente relazione:
Possiamo porre che:
Andando così ad ottenere:
La prima equazione è detta equazione canonica dell'iperbole riferita ai propri assi; mentre il numero è la metà della differenza delle distanze di ogni punto dai due fuochi, il numero
ha un significato geometrico che si capisce meglio studiando le proprietà delle iperboli.
Osservazioni finali
Osservazione 4:
Nel caso in cui i fuochi
ed
siano presi ancora equidistanti dall'origine, ma situati sull'asse delle ordinate, per semplicità porremo
. A questo punto, seguendo passaggi molto simili a quelli precedenti e ponendo sempre
, otterremo l'equazione:
con la differenza che mentre nella prima equazione risultava
, nella seconda equazione vale invece
. Il segno meno scaturisce dall'ultimo passaggio che ha consentito di ottenere la prima equazione: com'è chiaro questa inversione di coordinate lascia il termine in
negativo e quello in
positivo; la seconda equazione viene allora ottenuta semplicemente cambiando i segni a tutta l'equazione. È chiaro infine che in questo caso le coordinate dei fuochi sono
ed
.
Osservazione 5
Il segno meno inizialmente presente all'interno del valore assoluto viene trasformato in un segno più dalle successive due elevazioni al quadrato. Ciò significa che, a partire dalla seconda elevazione e fino all'ultimo passaggio, i calcoli effettuati sono formalmente identici a quelli svolti per ricavare l'equazione dell'ellisse. Il risultato ottenuto è diverso solo in virtù dell'osservazione 1, che ci consente di adoperare la disuguaglianza triangolare nel "verso opposto".
Altro materiale di supporto
Videolezione sull'iperbole
Esercizio proposto
Determinare l'equazione dell'iperbole passante per il punto
Consulta anche il formulario sull'iperbole.
Se hai dubbi o domande sull'argomento chiedi pure nella sezione geometria e algebra lineare del nostro forum!
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
