Equazione e caratteristiche della Parabola

In questo appunto di Geometria daremo una descrizione dettagliata della Parabola, partendo dalla definizione ed equazione, per poi analizzarne i punti caratteristici.

La parabola: definizione ed equazione generale

Per definizone, la parabola è quel luogo geometrico dei punti del piano cartesiano che sono equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.

conseguentemente, data una retta d direttrice ed un fuoco F, la parabola è formata da tutti i punti P tali che:

Oltre a Fuoco e Direttrice, un altro punto caratteristico della parabola è il vertice V in quanto rappresenta il rappresenta il punto più in basso della parabola quando è rivolta verso l’alto, viceversa, rappresenta il punto più in alto quando è rivolta verso il basso.
La parabola, così come la circonferenze, l'ellisse e l'iperbole, fa parte delle curve che prendono il nome di coniche non degeneri, in quanto sono curve date dall'intersezione tra un piano e un cono a due falde.

Detto

l'angolo tra l'asse del cono e le sue rette generatrici (guarda la figura), se prendiamo un piano che forma un angolo pari ad

con l'asse, allora l'intersezione tra questo angolo e il piano genera una parabola.

Se consideriamo una direttrice orizzontale, quindi di equazione del tipo

, allora la parabola avrà come asse di simmetria un asse perpendicolare all'asse x e parallelo all'asse y; viceversa, se consideriamo una direttrice di equazione

, allora la parabola avrà un asse di simmetria parallelo all'asse x e perpendicolare all’asse y.
Adesso entriamo più nel dettaglio e vediamo quale è l’equazione generica di una parabola con asse di simmetria del tipo

, cioè considereremo il primo caso (il secondo sarà analogo, basterà scambiare il ruolo della x con quello della y e viceversa).
L'equazione generica di una parabola è del tipo:

.

Come possiamo vedere, si tratta di un’equazione di secondo grado in x, con a,b e c coefficienti numerici reali. Questi coefficienti possono assumere qualunque valore e, dipendentemente dal valore di questi coefficienti, avremo delle particolari caratteristiche della parabola; tuttavia, l’unica condizione di esistenza della parabola è che

, altrimenti non avremmo più un’equazione di secondo grado e, conseguentemente, non avremmo più una parabola bensì l’equazione di una retta:

Analizziamo adesso il significato e le particolarità di questi coefficienti.
In particolare, dipendentemente dal segno del coefficiente a, cambia la concavità della parabola. In particolare, avremo che:

• se
  [math]a>0[/math]
  allora la parabola è rivolta verso l'alto e il vertice V rappresenta il punto più basso della parabola;
• se
  [math]a>0[/math]
  allora la parabola è rivolta verso il basso e il vertice V rappresenta il punto più alto della parabola.

Il coefficiente c, invece, fornisce informazioni sul punto di intersezione della parabola con l’asse y, ovvero dove la parabola taglia l'asse delle y.
Dopo questa breve introduzione sulla parabola, nel prossimo paragrafo vedremo quali sono i punti caratteristici di una parabola, nonché le formule più importanti per determinarli.

Caratteristiche Fondamentali della Parabola

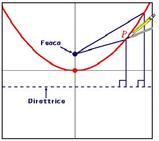
Consideriamo la generica parabola in figura:

Come accennato in precedenza, il fuoco F, la direttrice d e il vertice V sono le caratteristiche fondamentali della parabola. Nota l’equazione della parabola, possiamo determinare le equazioni o formule di quest’ultimi ricorrendo al discriminante di un’equazione di secondo grado associata all’equazione della parabola, ovvero:

In questo caso, vertice, direttrice e fuoco possono essere determinati tramite le seguenti formule:

Di conseguenza, dipendentemente dal valore del discriminante possiamo avere i seguenti casi particolari:

- se
[math]\Delta>0 [/math]
allora la parabola non interseca l'asse x;
- se
[math]\Delta>0 [/math]
allora la parabola interseca l'asse x in due punti;
- se
[math]\Delta=0 [/math]
allora il vertice della parabola è l'unico punto che la parabola ha in comune con l'asse x.

Inoltre, un caso particolare è dato dal caso in cui

poiché otteniamo una parabola rivolta verso l’alto, con asse di simmetria coincidente con l’asse y e vertice coincidente con l’origine degli assi cartesiani. In questo caso, l’equazione della parabola si riduce a:

In tutti questi esempi abbiamo considerato il caso in cui la parabola ha asse di simmetria parallelo all’asse y; nel prossimo paragrafo vedremo il caso in cui invece, l’asse di simmetria è parallelo all’asse x.

Parabola con asse parallelo all’asse x

In questo paragrafo vedremo quanto detto nei paragrafi precedenti, considerando però il caso in cui la parabola abbia l’asse di simmetria parallelo all’asse delle ascisse. In questo caso l’equazione della parabola sarà:

.

Si tratta sempre di un’equazione di secondo grado, ma non più in x, bensì in y, con a,b e c sempre coefficienti numerici reali. Anche in questo caso i coefficienti possono assumere qualunque valore e, dipendentemente dal valore di questi coefficienti, avremo delle particolari caratteristiche della parabola; tuttavia, l’unica condizione di esistenza della parabola è che

,poiché se

, otteniamo nuovamente una retta.
Dipendentemente dal segno del coefficiente a, cambia la concavità della parabola. In particolare, avremo che:

• se
  [math]a>0[/math]
  allora la parabola è rivolta verso destra e il vertice V rappresenta il punto più a sinistra della parabola (estremo sinistro);
• se
  [math]a>0[/math]
  allora la parabola è rivolta verso sinistra e il vertice V rappresenta il punto più a destra della parabola (estremo destro).

Similarmente, il coefficiente cfornisce informazioni sul punto di intersezione della parabola con l’asse x.
Vediamo adesso come cambiando le formule di fuoco F, direttrice d e vertice V (l’espressione del discriminante non cambia, rimane sempre

); quindi avremo che:

Anche in questo caso abbiamo i seguenti casi particolari:

- se
[math]\Delta>0 [/math]
allora la parabola non interseca l'asse y;
- se
[math]\Delta>0 [/math]
allora la parabola interseca l'asse y in due punti;
- se
[math]\Delta=0 [/math]
allora il vertice della parabola è l'unico punto che la parabola ha in comune con l'asse y.

Inoltre, un caso particolare è dato dal caso in cui

poiché otteniamo una parabola rivolta verso destra, con asse di simmetria coincidente con l’asse x e vertice coincidente con l’origine degli assi cartesiani. In questo caso, l’equazione della parabola si riduce a:

Visti entrambi i casi passiamo al prossimo paragrafo, dove sono presenti dei link di approfondimento per gli argomenti trattati in questo appunto.

Approfondimenti

Per ulteriori approfondimenti di quanto detto, si consiglia la lettura dei seguenti appunti:

• discriminante di una conica
• ellisse
• circonferenza
• Parabola
• Fuoco e direttrice di una parabola