Area del cerchio - Brevi richiami di teoria

In questo appunto viene descritta l'area del cerchio, con attenzione particolareggiata agli elementi principali, come ad esempio l'area del cerchio con brevi richiami di teoria, la circonferenza come luogo geometrico dei punti del piano, il cerchio corda e diametro per ripassare le definizioni di base, la formula principale dell’area del cerchio e sua derivazione.

Area del cerchio, brevi richiami di teoria per le definizioni di base

Prima di arrivare alle formule, che spesso vanno giù a memoria come le tabelline, facciamo un breve ripasso di teoria.

Se però conosci il significato dei termini: "cerchio", "circonferenza" o "raggio", puoi saltare la prima parte e andare direttamente alle formule. L’appunto è suddiviso in piccoli paragrafi nei quali sono stati raccolti gli elementi necessari per la comprensione della formula e del suo utilizzo.

per ulteriori approfondimenti vedi anche qua

Circonferenza come luogo geometrico dei punti del piano

Iniziamo con la definizione di luogo geometrico che ci consente di definire poi la circonferenza. In geometria con la dicitura luogo geometrico, si indica un insieme di punti che godono tutti di una stessa proprietà. Qual è la proprietà dei punti che appartengono alla circonferenza? Pensiamo a quando usiamo il compasso, fissiamo una delle due aste in un punto (che sarà il centro) e con l’altra che contiene la mina stabiliamo il raggio, quindi tracciamo la nostra circonferenza bella precisa. Abbiamo applicato la definizione di luogo geometrico tracciando un insieme di punti equidistanti dal punto O. Diamo allora la definizione: la circonferenza è una linea chiusa, i cui punti sono tutti equidistanti da un punto O detto centro e questa distanza è il segmento che chiamiamo raggio r. Altri luoghi geometrici del piano sono ad esempio l’asse di un segmento, definito come luogo dei punti del piano equidistanti dagli estremi del segmento stesso, e la bisettrice di un angolo definita come luogo dei punti del piano equidistanti dai lati dell’angolo.

Cerchio corda e diametro per ripassare le definizioni di base

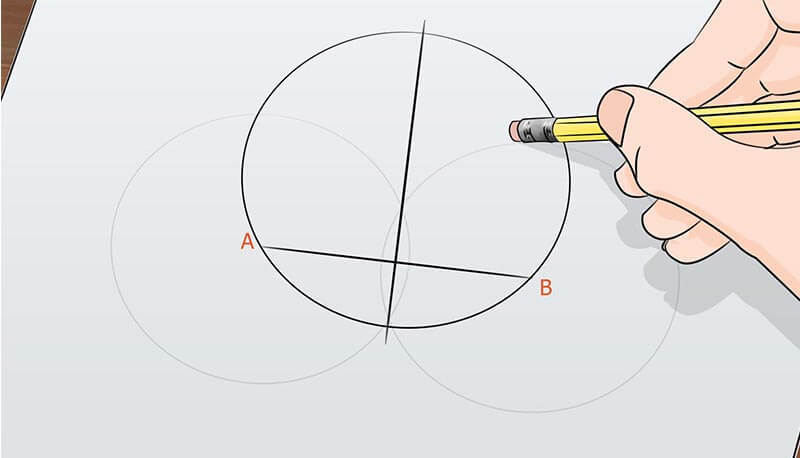
Il cerchio è definito come la parte di piano racchiusa dalla circonferenza, il cerchio comprende sia i punti della circonferenza che quelli interni ad essa. Con cerchio si intende perciò sia il bordo che quello che sta all’interno. Unendo due punti AB di una circonferenza, come in figura, si ottiene un segmento che si definisce corda, all’aumentare della distanza tra i punti si ottengono corde sempre più grandi, se questa corda passa per il centro, si ha la massima lunghezza. La corda massima è nota come diametro, la cui lunghezza è pari al doppio del raggio, usando come di consueto la lettera d in minuscolo oppure in maiuscolo D, abbiamo:

Area e superficie, non confondere una grandezza fisica e la sua unità di misura

Per area di una figura piana si intende la misura della sua superficie, quindi attenzione a non fare confusione, area e superficie non sono sinonimi. La superficie è la parte di piano che dobbiamo misurare, ovvero il cerchio sopra definito, l’area è la misura di questa superficie. L’area è una grandezza derivata, ha le dimensioni di una lunghezza al quadrato, ad esempio il metro quadrato oppure usando i sottomultipli del metro come il centimetro quadrato e così via.

Formula principale dell’area del cerchio e sua derivazione

L’area di un cerchio è uguale al quadrato della misura del raggio moltiplicato per pi greco, in simboli dunque:

Perché si usa questa la formula? Un cerchio può essere considerato come un poligono con infiniti lati, inscritto in una circonferenza il cui apotema è congruente al raggio. All’aumentare dei punti il poligono viene a coincidere con la circonferenza. L’area di un poligono inscritto è pari al prodotto del suo perimetro per l’apotema il tutto diviso per 2:

Per un cerchio il perimetro è la misura della lunghezza della circonferenza C, e l’apotema corrisponde al raggio r, abbiamo allora:

Sappiamo poi che la lunghezza della circonferenza è data da:

sostituendo:

semplificando, otteniamo infine:

Che è la formula per il calcolo dell'area del cerchio, nota fin dalla quinta elementare.

Formule alternative per il calcolo dell’area del cerchio

Per la relazione che sussiste tra raggio e diametro, sappiamo che:

sostituendo nella formula principale dell’area:

Esprimendo il raggio in funzione della circonferenza C abbiamo:

sostituendo sempre al posto di r, nella formula principale:

In questo modo è possibile calcolare direttamente l’area conoscendo la misura della circonferenza.

Formula inversa per ricavare il raggio estraendo la radice quadrata

Nei problemi di geometria a volte la consegna richiede l’uso delle formule inverse ovvero l’area è data ma bisogna calcolare il raggio. Poiché questo è al quadrato, è necessario estrarre la radice quadrata, che è l’operazione inversa della potenza di ordine 2. A mio avviso è importante saper manipolare le formule per ricavare le varie grandezze che vi compaiono, in modo da evitare di dover mandare a memoria o di ricorrere a tabelle precompilate, soprattutto quando le formule sono elaborate e contengono molte grandezze relazionate tra loro da varie operazioni. Ricaviamo allora la formula inversa. Osserviamo che il raggio è moltiplicato per

, il raggio è la nostra incognita e quindi applicando il secondo principio di equivalenza delle equazioni, dividiamo i due membri per

,

da cui otteniamo:

ed ora estraiamo la radice ai due membri:

al primo membro la radice è esatta, otteniamo infine:

che è la formula inversa per calcolare il raggio.