Volume tronco di cono - Formula e spiegazione

In questo appunto viene descritta la formula per il calcolo del volume di un tronco di cono; per comprendere meglio tale formula è prima utile ripassare brevemente le caratteristiche del cono e gli elementi fondamentali che lo costituiscono.

Il cono

Il cono è un solido di rotazione che viene generato dalla rotazione di un triangolo rettangolo intorno ad uno dei suoi cateti.

Ricordiamo brevemente che un triangolo rettangolo è un particolare tipo di triangolo caratterizzato da due angoli acuti e da un angolo retto (ampiezza di 90°); i lati del triangolo che definiscono l’angolo retto prendono il nome di cateti mentre il lato opposto al triangolo rettangolo prende il nome di ipotenusa.

Se si considera un triangolo rettangolo e si fa ruotare tale triangolo intorno ad uno dei suoi cateti (senza modificare le dimensioni del triangolo quindi eseguendo una rotazione rigida) si ottiene un particolare solido che prende il nome di cono.

Il cono è quindi un solido tridimensionale caratterizzato da una base circolare (formata dal cateto che non appartiene all’asse di rotazione) e da una superficie laterale.
Il vertice del triangolo che appartiene all’asse di rotazione non subisce spostamenti durante la trasformazione rigida e definisce un punto, chiamato vertice del cono, che ha la proprietà di essere il punto più distante dalla superficie di base.

Gli elementi fondamentali che costituiscono il cono sono quindi il raggio della base, che corrisponde alla lunghezza del cateto che non appartiene all’asse di rotazione e l’altezza, ovvero la distanza tra la base e il vertice del cono (punto che corrisponde anche ad un vertice del triangolo generatore).
L’altezza viene costruita tracciando quel segmento che ha come estremo il vertice del cono e che cade perpendicolarmente alla base (cioè forma, all’intersezione con la base, tutti angoli retti).

In precedenza è stato detto che la superficie di base di un cono è un cerchio; ricordiamo le l’area di un cerchio (S) può essere calcolata, noto il raggio, tramite la seguente espressione:

Dove π (pi greco) è un numero irrazionale che corrisponde a 3,14…
Per ulteriori approfondimenti sulla definizione di rotazione rigida e sulle equazioni che la descrivono vedi anche qua
Per ulteriori approfondimenti sul π e le sue caratteristiche vedi anche qua

Volume tronco di tronco di cono

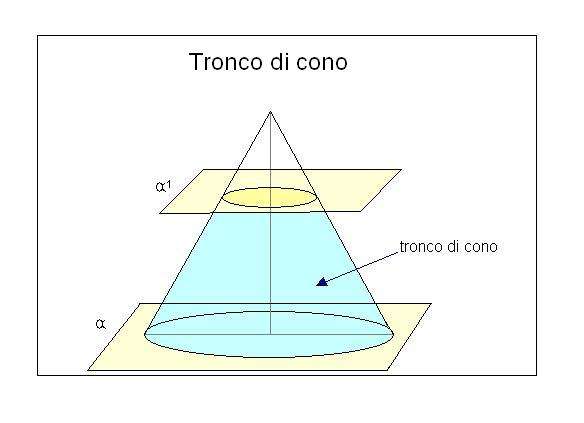
Consideriamo un cono, se esso viene tagliato da un piano parallelo alla base e non passante per il vertice, si formeranno due figure solide: un cono di dimensioni minori in alto ed un tronco di cono in basso.
Un tronco di cono è quindi la parte di cono delimitata da due piani paralleli che non contiene il vertice.
Questa figura sarà delimitata da due cerchi (aventi circonferenze simili) che prendono il nome di basi, chiamiamo S la base superiore e con s la base inferiore.

Un’altra proprietà è che le due circonferenze saranno proporzionali alle distanze delle circonferenze stesse dal vertice:

(dove H non è altro che l'altezza del cono prima che venisse tagliato dal piano parallelo e h è l’altezza della circonferenza minore dal vertice del cono).

Si può dimostrare inoltre che le superfici delle due circonferenze di base, sono direttamente proporzionali ai quadrati delle altezze; tale relazione espressa sottoforma di equazione matematica corrisponde a:

Dove x rappresenta l'altezza del tronco di cono.

Considerando la relazione appena riportata è possibile applicare la radice quadrata ai vari termini e riscriverla nel seguente modo:

Per la proprietà dello scomporre è possibile ottenere tale relazione:

Da tale relazione è possibile esplicitare la grandezza x:

Il volume totale risulta quindi essere pari a:

Il risultato finale che si ottiene dopo qualche passaggio matematico è:

Il volume del cono è relazionato all’altezza del tronco di cono (h) e ai raggi delle circonferenze che definiscono la base (R è il raggio della base maggiore mentre r è il raggio della base minore).
Per calcolare il volume del tronco di cono è quindi necessario conoscere il valore dell’altezza del tronco di cono e i valori dei raggi delle circonferenze che individuano le basi.

Osservando la formula che esprime il volume di un tronco di cono si può notare come tale grandezza sia direttamente proporzionale all’altezza del cono (maggiore è l’altezza del cono e maggiore sarà il volume del cono considerato).
Il volume del tronco di cono è anche proporzionale ai raggi delle superfici di base, in tal caso la proporzionalità è più complessa perché sono presenti tre termini che contengono i raggi.

A volte può essere utile calcolare l’altezza del tronco di cono, noto il volume e noti i raggi delle due circonferenze di base; per fare ciò è utile ricavare la formula inversa che esprime l’altezza del tronco di cono: