In questo appunto di matematica affronteremo una figura solida molto comune, la piramide, descrivendone le caratteristiche e le formule fondamentali.
Indice
La piramide
In geometria si definisce piramide un poliedro individuato da una faccia poligonale chiamata base e da un vertice che non giace sul piano della base e che talora viene chiamato apice della piramide.
Sono facce della piramide la sua base e le facce triangolari (chiamate facce laterali).
Allo stesso modo diremo che una piramide è un poliedro limitato da un poligono e dai triangoli ottenuti congiungendo un punto, non appartenente al piano del poligono, con i vertici del poligono stesso.
La piramide prende il suo nome dal numero di lati del poligono di base, per cui diremo:
- piramide triangolare, se la base è un triangolo;
- piramide quadrangolare, se la base è un quadrangolo;
- piramide pentagonale, se la base è un pentagono;
- piramide esagonale, se la base è un esagono;
- ecc…
I lati ed il vertici del poligono di base si chiamano rispettivamente spigoli e vertici di base;
i rimanenti lati dei triangoli ed il punto ad essi comune si chiamano, rispettivamente, spigoli laterali e vertice; l’altezza della piramide è la distanza fra il vertice ed il piano del poligono di base.
La superficie laterale di una piramide si ottiene dalla somma delle superfici dei triangoli, mentre l’area di base è costituita dall’area del poligono di base.
Una piramide è una figura convessa, poiché può essere definita come intersezione di due figure convesse: un angoloide ed un semispazio.
Proprietà della piramide
Consideriamo una piramide qualunque di vertice V.
Se dal piede H dell’altezza VH si conduce il segmento HK di perpendicolare alla retta dello spigolo di base AB, il segmento VK è perpendicolare ad AB, ossia è l’altezza relativa al lato AB della faccia VAB della piramide.
Tale proprietà è una diretta conseguenza del teorema delle tre perpendicolari.
Una seconda importante proprietà che vale in generale per tutte le piramidi viene espressa tramite un teorema la cui dimostrazione sarà affrontata in altra sede.
Tale teorema afferma che sezionando una piramide di vertice V e base P = ABC… con un piano parallelo a P si ottiene un poligono
P_1 = A_1B_1C_1…
[/math]
simile a P; i perimetri di
P
[/math]
e
P_1
[/math]
stanno fra loro come le rispettive distanze da V, mentre
P
[/math]
e
P_1
[/math]
stanno fra loro come i quadrati costruiti si tali distanze:
2p(P) : 2p(P_1) = VH : VH_1
[/math]
inoltre
P : P_1 = (VH)^2 : (VH_1)^2
[/math]
dove
2p(P)
[/math]
è il perimetro di P
2p(P_1)
[/math]
è il perimetro di P_1.
Piramide retta
Nell’insieme delle piramidi esiste un sottoinsieme i cui elementi hanno le seguenti caratteristiche:
- la base è un poligono apotemato, ossia circoscrivibile ad un cerchio;
- l’altezza della piramide ha come piede il centro del suddetto cerchio.
Agli elementi di tale sottoinsieme si da il nome di piramidi rette.
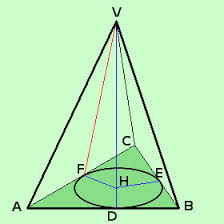
Diremo che una piramide è retta quando ha per base un poligono circoscrivibile ad un cerchio ed il centro O di tale cerchio è il piede dell’altezza.
Se in una piramide retta ha per base un poligono regolare, diremo che tale piramide è regolare.
In questo tipo di piramidi le altezze delle facce laterali (relativi agli spigoli della base) sono tutte uguali fra loro e prendono il nome di apotema della piramide. Si noti che le piramidi non retta non hanno apotema perché le loro facce laterali hanno generalmente altezze disuguali.
Nelle piramidi regolari anche gli spigoli laterali sono tutti uguali fra loro, per cui le facce laterali sono triangoli isosceli uguali.
Consideriamo ora una piramide retta dove a è il suo apotema,
2p
[/math]
il perimetro della base,
l_1
[/math]
,
l_2
[/math]
, …;
l_n
[/math]
le lunghezze dei suoi spigoli di base.
Siano inoltre
A_l
[/math]
l’area delle superfici laterali
A_t
[/math]
l’area della superficie totale
B
[/math]
l’area della base.
Poiché le facce laterali sono triangoli aventi tutti altezza lunga a, si ha che:
A_l = (\frac{1}{2})(a l_1) + (\frac{1}{2})(a l_2) + … + (\frac{1}{2})(a l_n) =
[/math]
= (\frac{1}{2})(a)(l_1 + l_2 + … + l_n) =
[/math]
= (\frac{1}{2})(a)(2p) =
[/math]
= a p
[/math]
quindi si ha che
A_t = a p + B
[/math]
Problemi relativi alle piramidi
Relazione fra apotema altezza ed apotema di base di una piramide retta.
Si consideri una piramide retta a base triangolare. Il triangolo VHK, avente come vertici il vertice della piramide V, il piede della sua altezza, H, ed il piede dell’altezza di una sua faccia e formato dall’altezza, dall’apotema di base (raggio del cerchio inscritto) e dall’apotema della piramide, è un triangolo rettangolo con l’angolo retto in H.
Applicando il Teorema di Pitagora si ha che:
(VK)^2 = (VH)^2 + (HK)^2
[/math]
avendo posto
a = apotema
h = altezza
r = apotema di base
si ha che
a = \sqrt[2]{h^2 + r^2}
[/math]
ed inversamente
h = \sqrt[2]{a^2 - r^2}
[/math]
r = \sqrt[2]{a^2 - h^2}
[/math]
Se la piramide è regolare avremo i seguenti casi:
- se la base è un triangolo equilatero, l’apotema di base è la terza parte dell’altezza del triangolo
[math];
r = \frac{h_t}{3}
[/math] - se la base è un quadrato, l’apotema di base è la metà del lato l di base
[math];
r = \frac{l}{2}
[/math] - se la base è un esagono regolare l’apotema di base si ottiene ricordando che il lato dell’esagono regolare è uguale al suo raggio
[math];
r = \frac{l \sqrt[2]{3}}{2}
[/math] - se la base è un poligono regolare qualunque, l’apotema di base si ottiene, come già sapete moltiplicando la misura l del lato per il valore k del corrispondente numero fisso
[math].
r = (k)(l)
[/math]
Si consideri una piramide retta a base quadrangolare. Il triangolo VHB, avente come vertici il vertice della piramide V, il piede della sua altezza, H, ed il piede dell’altezza di una sua faccia e formato dall’altezza, dall’apotema di base (raggio del cerchio inscritto) e dallo spigolo della piramide, è un triangolo rettangolo con l’angolo retto in H.
Applicando il Teorema di Pitagora si ha che:
(VB)^2 = (VH)^2 + (HB)^2
[/math]
avendo posto
s = spigolo
h = altezza
R = raggio del cerchio circoscritto alla base della piramide
si ha che
s = \sqrt[2]{h^2 + R^2}
[/math]
h = \sqrt[2]{s^2 - R^2}
[/math]
R = \sqrt[2]{s^2 - h^2}
[/math]
Se la piramide è regolare si hanno i seguenti casi:
- se la base è un triangolo equilatero, il raggio di base è pari ai 2/3 dell’altezza di base del triangolo
[math];
R = \frac{2 h_t}{3}
[/math] - se la base è un quadrato, il raggio di base è uguale alla metà della diagonale d di base
[math];
R = \frac{d}{2}
[/math] - se la base è un esagono regolare, il raggio di base è uguale al lato l dell’esagono stesso
[math];
R = l
[/math] - se la base è un poligono regolare qualunque, il raggio di base si ottiene applicando il Teorema di Pitagora al triangolo rettangolo avente come cateti l’apotema di base e la metà del lato e come ipotenusa il raggio stesso.
Si consideri una piramide regolare a base (ad esempio) esagonale. Essendo ogni faccia della piramide regolare è un triangolo isoscele ed il suo apotema è rappresentato dall’altezza di uno di tali triangoli, si osserva che questo divide ogni faccia laterale in due triangoli rettangoli tra loro congruenti.
Il triangolo VAK, avente come lati l’apotema, metà del lato di base e lo spigolo laterale, è rettangolo, con l’angolo retto in K.
Applicando il Teorema di Pitagora si ha che:
(VA)^2 = (VK)^2 + (AK)^2
[/math]
avendo posto
s = spigolo laterale
a = apotema
l = lato di base
si ha che
s = \sqrt[2]{a^2 + (\frac{l}{2})^2}
[/math]
a = \sqrt[2]{s^2 - (\frac{l}{2})^2}
[/math]
\frac{l}{2} = \sqrt[2]{s^2 - a^2}
[/math]
Area laterale ed area totale di una piramide retta
Sia data una qualunque piramide retta. Lo sviluppo sul piano della superficie laterale è composto da tanti triangoli quanti sono i lati di base della piramide. Tali triangoli hanno:
- altezze tra loro congruenti ed una qualsiasi di esse costituisce l’apotema della piramide;
- basi rispettivamente congruenti a ciascuno dei lati di base.
Se ne conclude che la superficie laterale,
A_l
[/math]
, di una piramide retta è equivalente ad un triangolo avente come base il perimetro di base,
2p
[/math]
, e per altezza l’apotema,
a
[/math]
, della piramide:
A_l = \frac{(2p)(a)}{2}
[/math]
quindi l’area di una piramide retta si calcola dividendo per due il prodotto del perimetro di base per la misura dell’apotema.
Le formule inverse ci forniscono:
2p = \frac{(2)(A_l)}{a}
[/math]
a = \frac{(2)(A_l)}{2p}.
[/math]
Se la piramide è regolare, continuano a valere queste formule.
Se la piramide non è retta, l’area laterale si ottiene sommando tra loro le aree di ciascuna delle facce laterali.
L’area totale,
A_t
[/math]
, di una piramide si ottiene sommando l’area laterale,
A_l
[/math]
, all’area di base,
A_b
[/math]
:
A_t = A_l + A_b
[/math]
Le formule inverse forniscono:
A_l = A_t - A_b
[/math]
A_b = A_t + A_l
[/math]
Volume di una piramide
Al fine di determinare sperimentalmente il volume di una piramide, si può confrontare il volume di tale solido con quello di un prisma avente la stessa base e la stessa altezza.
Supponiamo di avere a disposizione un contenitore cilindrico graduato contenente un liquido e tale che le sue dimensioni possano permettere di contenere abbondantemente sia il prisma che successivamente la piramide.
Se si immergono prima la piramide e poi il prisma si nota che l’innalzamento di liquido dovuto al prisma è tre volte quello causato dalla piramide: da tale esperienza se ne conclude che il volume della piramide è 1/3 quello del prisma retto avente la stessa base e la stessa altezza della piramide.
Una piramide è equivalente alla terza parte di un prisma avente la stessa base e la stessa altezza.
V = \frac{(h)(A_b)}{3}
[/math]
V
[/math]
= volume della piramide
A_b
[/math]
= area di base
h
[/math]
= altezza della piramide
Il volume della piramide si ottiene dividendo per tre il prodotto dell’area di base per la misura dell’altezza.
Le formule inverse ci forniscono:
A_b = \frac{(3)(V)}{h}
[/math]
h = \frac{(3)(V)}{A_b}.
[/math]
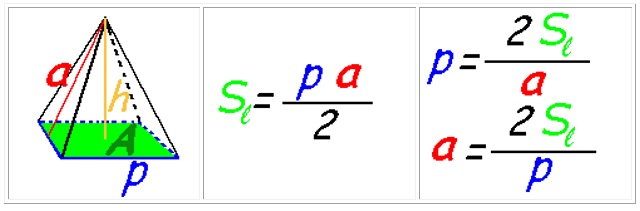
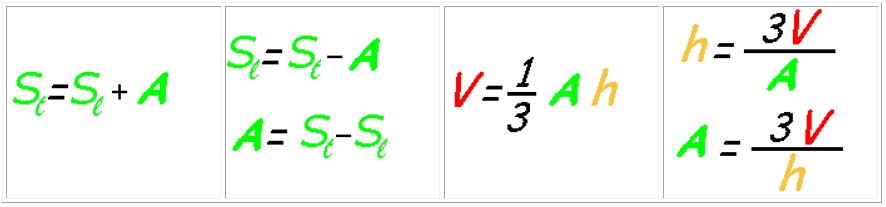
6 Talete e l'altezza della piramide di Cheope
Si racconta (Plutarco e Plinio il vecchio) che il faraone Amasis, abbia sfidato Talete a
misurare l'altezza della piramide di Cheope.
È possibile misurare l'altezza di un monumento senza salirci sopra? Talete fu il primo a riuscirci nel VI secolo a.C., grazie a una felice intuizione. Egli si accorse, infatti, che la lunghezza di un'ombra proiettata sul terreno dipende dall'altezza dell'oggetto che l'ha originata secondo una relazione matematica ben precisa. In particolare, se si confrontano le ombre di due oggetti diversi, queste stanno tra loro come le altezze degli oggetti corrispondenti:
lunghezza ombra 1 : lunghezza ombra 2 =
= altezza oggetto 1 : altezza oggetto 2
Conoscendo l'altezza di un'asta usata per il confronto e misurando le lunghezze delle ombre sul terreno, Talete fu in grado di determinare l'altezza della piramide.
lunghezza ombra 1 : lunghezza ombra 2 =
= altezza asta : altezza incognita della piramide
Non avendo neanche unità di misura adatte per i suoli calcoli Talete introdusse il talete, unità di misura equivalente alla propria altezza.
Il cosiddetto Teorema di Talete è la formalizzazione di questa intuizione.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
