Esagono: regole e formule

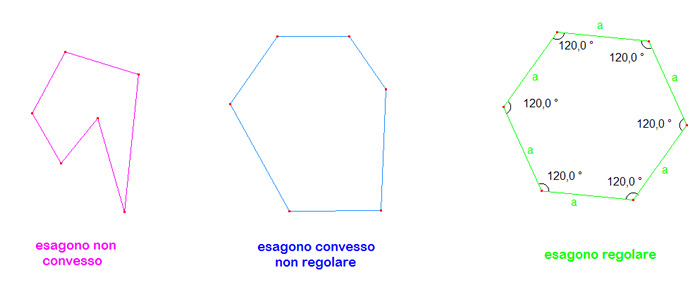
In questo appunto viene descritto l'esagono. Ricorda che si definisce esagono un qualsiasi poligono avente 6 lati, non necessariamente della stessa lunghezza, e 6 vertici. Se poi i lati hanno tutti la stessa lunghezza e tutti gli angoli sono congruenti, allora si parla di esagono regolare.

Definizione

L'esagono è un poligono piano avente sei lati e sei vertici. Può essere convesso, concavo o intrecciato.

La parola esagono è l'unione delle parole exi, che significa sei e gonia, che vuol dire angolo.

L'esagono regolare è un poligono regolare avente 6 lati.

Ricorda che un poligono si dice regolare quando ha tutti i lati e tutti gli angoli congruenti.

Per ulteriori approfondimenti sui poligoni regolari vedi anche qua

Proprietà

Elenchiamo, in questo paragrafo, alcune importanti proprietà degli esagoni regolari.
Ciascuno degli angoli interni di un esagono regolare misura 120°.

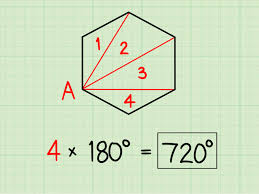
Questo risultato può essere ottenuto facilmente. Come si sa, secondo un noto teorema, la somma degli angoli interni di un poligono regolare è pari a tanti angoli piatti quanti sono i lati del poligono meno due.

Dal momento che l'esagono ha sei lati, la somma dei suoi angoli interni è pari a:

Ciascuno degli angoli interni sarà quindi ampio:

.

Un esagono regolare possiede nove diagonali, non tutte passanti per il centro.

Ricorda, infatti, che il numero delle diagonali di un qualsiasi poligono di n lati si può ottenere mediante la formula:

Un esagono regolare, come tutti i poligoni regolari, si può sia inscrivere che circoscrivere ad una circonferenza.

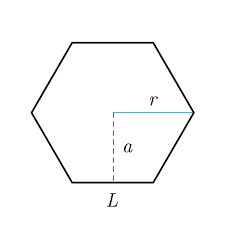
Il lato dell'esagono regolare, inscritto in una circonferenza, è pari al raggio.

Questa proprietà, molto peculiare, si può dimostrare facilmente. Tracciando tutte le diagonali che passano per il centro, si generano sei triangoli uguali. In questo modo, l'angolo al centro O risulta diviso in sei parti uguali, ciascuna ampia 60°. Ricordando che la somma degli angoli interni di un triangolo è sempre 180°, ciascuno dei due angoli alla base, congruenti tra loro, sarà 60°. Ecco così ottenuto un triangolo equilatero, che avrà uno dei tre lati coincidente con il lato dell'esagono e gli altri due con il raggio della circonferenza circoscritta.

L'apotema di un esagono regolare, cioè il lato della circonferenza inscritta in esso, è pari all'altezza di ciascuno dei triangoli equilateri che si formano tracciando le diagonali.

La somma degli angoli esterni di un esagono regolare è pari a un angolo giro.

Un esagono regolare ha 6 assi di simmetria e un centro di simmetria, che coincide con il centro della figura.

Formule utili

Questo paragrafo costituisce una nutrita raccolta di formule utili per risolvere i problemi che coinvolgono gli esagoni regolari.

Perimetro

Dal momento che è una figura regolare, per ottenere il perimetro di un esagono regolare basta moltiplicare per 6 la lunghezza del suo lato L.

Apotema

La misura dell'apotema dell'esagono regolare si può ottenere moltiplicando la lunghezza del lato L per il numero fisso f, che per l'esagono vale:

Ricorda che il numero fisso è il rapporto tra il lato di un poligono regolare ed il suo apotema. Ciascun poligono regolare ha un numero fisso diverso.

Area

[math]A = \frac{2p \cdot a}{2}[/math]

Area

[math]A = \varphi \cdot L^2[/math]

Come vedi, esistono due diverse formule per calcolare la misura dell'esagono. La prima richiede la conoscenza del perimetro e dell'apotema, e l'area sarà data dal loro prodotto diviso per due; per la seconda è necessario conoscere il lato e il valore

, cioè la cosiddetta costante d'area.

La costante d'area per l'esagono vale

. Anche questa, così come il numero fisso, dipende esclusivamente dal numero dei lati del poligono a cui si riferisce.

Esagono regolare inscritto e circoscritto ad una circonferenza

Riepiloghiamo, in questo paragrafo, tutte le considerazioni e le formule che possono essere utili quando ci si trova davanti a problemi con un esagono inscritto oppure circoscritto ad una circonferenza.

Esagono regolare inscritto in una circonferenza

Per quanto riguarda l'esagono inscritto in una circonferenza, abbiamo già detto che - congiungendo il centro dell'esagono otteniamo sei triangoli equilateri. Il raggio della circonferenza circoscritta avrà la stessa lunghezza del lato dell'esagono.
A partire da questa considerazione si può ottenere la misura dell'apotema a a partire da quello del raggio r (o del lato dell'esagono), che - in virtù di semplici considerazioni trigonometriche - è pari a:

Esagono regolare circoscritto ad una circonferenza

Anche in questo caso, congiungendo il centro della circonferenza con i vertici dell'esagono si ottengono 6 triangoli equilateri. In questo caso, però, il raggio r della circonferenza non coincide con il lato L dell'esagono. Ecco la formula per trovare il raggio:

Un problema di esempio

Per concludere questo appunto, mostriamo un problema di esempio, per poter osservare un utilizzo pratico delle formule studiate.

Problema: la somma delle dimensioni di un rettangolo è pari a 180 metri e sono una i 4/5 dell'altra. Calcola il perimetro dell'esagono regolare equivalente al rettangolo dato.

Svolgimento

Calcoliamo innanzitutto le dimensioni del rettangolo. Dal momento che una è i dell'altra, dividiamo il semiperimetro, , per per ottenere la lunghezza del segmento unitario, cioè . Le dimensioni saranno quindi:

Moltiplicandole tra di loro otteniamo

, l'area del rettangolo e anche dell'esagono ad esso equivalente.

A questo punto, utilizziamo le formule inverse per ottenere il lato L dell'esagono. Si ha:

Moltiplicando questo valore per 6 si ottiene il perimetro dell'esagono, come richiesto.

Per ulteriori approfondimenti sui problemi di geometria che coinvolgono gli esagoni vedi anche qua