Energia potenziale - regole

In questo appunto vengono descritti appieno i concetti di energia, il principio di conservazione dell’energia ed infine l’energia potenziale di un corpo, attraverso definizioni e concetti chiave fondamentali.

Energia

Esistono differenti forme di energia nel mondo fisico.

Si parla di energia cinetica, energia potenziale, che a sua volta può essere differenziata come energia potenziale elastica o energia potenziale gravitazionale. Per comprendere appieno i concetti relativi all’energia, è necessario avere chiari i fenomeni della cinematica e dinamica dei corpi, e pertanto tutti i concetti relativi anche al lavoro.
Qui di seguito si procede nella descrizione dei concetti fondamentali dell’energia potenziale elastica e dell’energia potenziale gravitazionale.

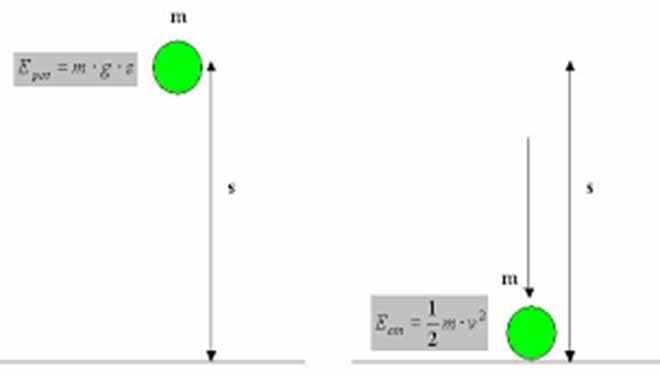
Per ulteriori approfondimenti sul concetto di lavoro e sul concetto energia, vedi qui

Energia potenziale gravitazionale

Indichiamo con ‘U’ l’energia gravitazionale. Maggiore è l’altezza e la massa di un maglio maggiore sarà l’energia potenziale con cui si conficcherà il corpo nel terreno.
Dato un corpo di massa m, si definisce energia potenziale gravitazionale del corpo e si indica con U, è il prodotto tra la massa, l'accelerazione di gravità e l'altezza, riportato così come segue:

Dove

è la massa del corpo in questione.
Dove

è l’accelerazione di gravità.
Dove

è l’altezza rispetto al livello di terra considerato di riferiento.

L’unità di misura dell’energia motenziale non è altro che pari a:

L’energia potenziale gravitazionale: viene trasmesso o assegnato dal lavoro che una persona compie, più sollevi un oggetto su più aumenterà la sua energia potenziale (verso il basso). Ricordando la relazione fondamentale per il calcolo del lavoro che una forza compie:

Questa si legge come il lavoro è uguale alla forza per lo spostamento.

Energia potenziale elastica

è un concetto fondamentale che deve essere chiarito in fisica. Si consideri una molla deformata è in grado di compiere lavoro una volta che è lasciata libera di tornare nella condizione di riposo; così anche per la forza elastica (che è un altro esempio di forza conservativa) è conveniente definire un’energia potenziale. Pertanto si va a concludere che per una molla con costante elastica k deformata di un tratto s, l’energia potenziale elastica vale la seguente relazione matematica riportata:

Dove

è l'energia potenziale elastica.
Dove

è la costante elastica della molla considerata.
Dove

è il livello di deformazione (allungamento) della molla.

Nella formula precedente il livello di zero dell’energia potenziale elastica è stato posto (come si fa abitualmente) nella condizione s = 0 m in cui la molla si trova a riposo.

Calcolo dell'energia potenziale elastica di una molla

Si consideri una molla con una costante elastica k = 96 N/m è allungata di 5,4 cm.
Il testo chiede di andare a calcolare e verificare quanto vale la sua energia potenziale in questa condizione appena descritta.
L’energia potenziale è data dalla formula precedente, da cui si ottiene pertanto che per la molla considerata deve valere quanto segue:

La definizione generale di energia potenziale

L’energia potenziale gravitazionale di un corpo è uguale al lavoro compiuto dalla forza-peso quando il corpo si sposta dalla posizione iniziale a quella di riferimento. Maggiore la massa e l’altezza maggiore sarà il lavoro che può compiere.
La definizione generale dell’energia potenziale è la seguente riportata.

Dove

è la variazione di energia potenziale.
Dove

è l'energia potenziale nella condizione finale.
Dove

è l'energia potenziale nella condizione iniziale.
Dove

è il lavoro svolto per passare dalla condizione iniziale alla condizione finale.

L’energia potenziale U può essere introdotta per tutte le forze conservative, generalizzando la definizione che abbiamo usato per la forza-peso. Per la definizione generale è stato considerato un sistema fisico che è soggetto alla forza conservativa. Esso si trova nella condizione iniziale A e passa poi nella condizione finale B.

Il principio di conservazione dell'energia in meccanica classica

Qui di seguito viene enunciato il principio di conservazione dell'energia alla base della meccanica classica. Il principio di conservazione verrà descritto partendo da un esempio pratico, per comprendere al meglio l'argomento.
Realizziamo un esperimento con un carrellino che si muova praticamente senza attrito. Esso è lasciato andare lungo il binario a partire da una determinata quota h e, dopo un certo tempo, risale dalla parte opposta raggiungendo la stessa quota.
Osservando il sistema si può effettuare una semplice e chiara osservazione.
SI osserva che quando il carrello parte da fermo, la sua energia cinetica è zero e quella potenziale mgh è massima; durante la discesa, l’energia potenziale diminuisce e quella cinetica aumenta; nel punto più basso l’energia cinetica è massima e quella potenziale è minima; durante la salita l’energia cinetica diminuisce mentre quella potenziale aumenta; quando il carrello si ferma di nuovo, la sua energia potenziale è la stessa che aveva all’inizio, mentre quella cinetica è di nuovo nulla.
Effettuando misure accurate si vede che le variazioni di energia cinetica e di energia potenziale non sono casuali: se gli attriti sono trascurabili, durante il moto l’energia cinetica e quella potenziale del carrello variano, ma la loro somma rimane costante.
Questa proprietà così importante suggerisce di definire una nuova grandezza fisica, l’energia meccanica totale, uguale alla somma dell’energia cinetica e di quella potenziale; allora il risultato sperimentale descritto sopra si può esprimere dicendo che: durante il moto di un sistema fisico senza attriti l’energia meccanica totale del sistema, somma dell’energia cinetica e dell’energia potenziale, si conserva.
Tornando all’esperimento del carrello, durante la sua discesa l’energia potenziale originale si trasforma progressivamente in energia cinetica; durante la salita, l’energia cinetica del carrello diminuisce e si trasforma in energia potenziale, fino ad annullarsi nel punto più alto della traiettoria, dove l’energia potenziale è massima.
Il principio di conservazione di energia potrebbe ricordare il principio di conservazione della massa del chimico Lavoisier.