Concetti Chiave
- L'esercizio analizza il campo elettrico generato da due cariche puntiformi in un mezzo dielettrico, utilizzando il Principio di Sovrapposizione degli Effetti.
- Due cariche, una nota e una incognita, sono poste a una distanza di 1,5m in un dielettrico con costante dielettrica relativa di 1,8, e il campo elettrico è nullo a 0,5m da una delle cariche.
- Per trovare la carica incognita, si utilizza la formula del campo elettrico e si impone la condizione di equilibrio, che porta a calcolare Q2 come 2,1•10^-2 C.
- Immersione nel vuoto non altera la posizione del punto dove il campo è nullo, poiché la relazione di equilibrio non dipende dalla costante dielettrica.
- La presenza di un dielettrico modifica l'intensità del campo elettrico e la forza di interazione tra le cariche, influenzando la polarizzazione del mezzo.
In questo appunto di fisica si affronta un semplice esercizio sul campo elettrico generato da due cariche puntiformi immerse in un mezzo isolante e poste ad una data distanza. Useremo il Principio di sovrapposizione degli effetti per studiare la condizione di equilibrio e ricavare le grandezze richieste.
Indice
Dati del problema
Siano date due cariche
Q_1 = 5,2•10^-3 C
[/math]
e
Q_2
[/math]
, incognita, poste in due punti del piano distinti, A e B rispettivamente, distanti L = 1,5m, ed immerse in un dielettrico il cui valore è
ε_r = 1,8
[/math]
.
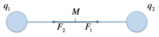
In un punto C, compreso fra gli estremi del segmento AB, e tale che AC = 0,5m il campo elettrico è nullo.
(supponiamo che la carica
Q_1
[/math]
si trovi in A alla sinistra dell’osservatore e la carica
Q_2
[/math]
in B, alla destra dell’osservatore).
Quesito 1: trovare il valore di
Q_2
[/math]
.
Quesito 2: se le due cariche fossero immerse nel vuoto, il campo elettrico sarebbe pari a zero nello stesso punto C?
Campo elettrico e Principio di Sovrapposizione degli Effetti
Data una qualunque carica Q, il campo elettrico che essa genera è dato in modulo dalla seguente espressione:
E = \frac{kQ}{R^2}
[/math]
dove
k = \frac{1}{4 π ε_0 ε_r }
[/math]
k = 9•10^9 Nm^2/C^2
[/math]
ε_0
[/math]
= costante dielettrica nel vuoto
ε_0 = 8,859•10^-12 C^2/Nm^2
[/math]
ε_r
[/math]
= costante dielettrica in un mezzo
R = distanza di un punto nello spazio dalla carica generatrice Q in cui si vuole conoscere il valore del campo elettrico
Le unità di misura sono riferite al Sistema Internazionale.
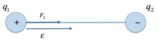
Poiché il campo elettrico è un campo vettoriale si deve definire anche la sua direzione (le linee di campo) ed il suo verso.
La direzione viene individuata da rette radiali che hanno come centro la carica generatrice Q chiamate linee di campo, mentre il verso dipende dal segno della carica Q.
Se la carica generatrice è positiva, le linee del campo elettrico saranno radiali uscenti, se è negativa saranno radiali entranti.
Osservando l’espressione che esprime il campo elettrico E si possono fare alcune osservazioni:
- il campo elettrico, a parità di distanza dalla carica generatrice, aumenta di intensità se aumenta il valore della carica che lo genera;
- il campo elettrico a parità di carica generatrice, diminuisce di intensità man mano che ci si allontana da questa, poiché è inversamente proporzionale al quadrato della distanza dalla carica;
- il campo elettrico è costante su superfici sferiche aventi il centro nella carica generatrice;
- la costante k non dipende dalle cariche ma dal mezzo in cui queste sono immerse .
Se si hanno più cariche in una stessa porzione di spazio i campi elettrici generati da ognuna di queste si sovrapporranno e si sommeranno vettorialmente. Ossia vale il Principio di Sovrapposizione degli Effetti:
date n cariche,
Q_1
[/math]
,..,
Q_n
[/math]
, agenti nello spazio, il campo elettrico in un punto P dello spazio, avente distanza
R_1
[/math]
,…,
R_n
[/math]
da ciascuna carica, si trova sommando vettorialmente i vettori campo elettrico in quel punto P, generati dalle varie cariche.
\vec{E_tot} = \vec{E_1}+…+\vec{E_n}
[/math]
rispettando le regole per eseguire il calcolo vettoriale.
Quesito 1
Il campo elettrico generato dalla carica
Q_1
[/math]
nel punto C è dato dalla seguente espressione:
E_1 = \frac{kQ_1}{(R_1)^2}
[/math]
dove
Q_1 = 5,2•10^-3 C
[/math]
R_1 = 0,5m
[/math]
k = \frac{1}{4 π ε_0 ε_r }
[/math]
Essendo
Q_1
[/math]
>0 (positiva) il verso delle linee campo del
E_1
[/math]
saranno uscenti dalla carica
Q_1
[/math]
. Affinché in C in campo si annulli, il vettore
E_2
[/math]
, campo elettrico generato dalla carica
Q_2
[/math]
, deve essere opposto ad
E_1
[/math]
: i campi devono essere opposti. Quindi possiamo asserire che la carica
Q_2
[/math]
deve essere anch’essa di segno positivo, poiché in questo caso le sue linee di campo sono radiali uscenti e nel punto C il vettore
\vec{E_2}
[/math]
è opposto al vettore
\vec{E_1}
[/math]
.
Si noti che avremmo ottenuto un risultato corretto anche se le due cariche fossero state entrambe negative: in questo caso i vettori che individuano i due campi nel punto C, avrebbero avuto linee di campo uscenti, ma sempre versi opposti.
Il valore del campo elettrico in C generato dalla carica
Q_2
[/math]
è dato da:
E_2 = \frac{kQ_2}{(R_2)^2}
[/math]
dove
Q_2
[/math]
= incognita
R_2
[/math]
= 1,0m poiché
R_2
[/math]
= L -
R_1
[/math]
k = \frac{1}{4 π ε_0 ε_r }
[/math]
Fissato un verso di percorrenza sul segmento AB che fissa come positivo il verso che va da A verso B (ossia da
Q_1
[/math]
a
Q_2
[/math]
, ossia da sinistra verso destra, nel verso di lettura) avremo che
E_1
[/math]
ha segno positivo, mentre
E_2
[/math]
ha segno negativo.
Il campo elettrico nel punto C si ottiene da
E_c
[/math]
=
E_1
[/math]
–
E_2
[/math]
E_c = \frac{kQ_1}{(R_1)^2} - \frac{kQ_2}{(R_2)^2}
[/math]
Essendo
E_c
[/math]
= 0
Si ha che
\frac{kQ_1}{(R_1)^2} - \frac{kQ_2}{(R_2)^2} = 0
[/math]
\frac{kQ_1}{(R_1)^2} = \frac{kQ_2}{(R_2)^2}
[/math]
\frac{Q_1}{(R_1)^2} = \frac{Q_2}{(R_2)^2}
[/math]
Q_2 = (R_2)^2 \frac{Q_1}{(R_1)^2}
[/math]
Sostituendo i valori numerici:
Q_2 = 2,08•10^-2 C
[/math]
approsimando
Q_2 = 2,1•10^-2 C
[/math]
Essendo
R_1
[/math]
= AC = 0,5 m
R_2
[/math]
= CB = 1,0 m
Q_1 = 5,2•10^-3 C
[/math]
Quesito 2
Se le due cariche non fossero immerse in un dielettrico, il campo sarebbe ancora nullo nel punto Cche dista 0,5m dalla carica Q_1, poiché la relazione di equilibrio non dipende dalla costante k che a sua volta dipende dal dielettrico
ε_r
[/math]
= 1,8.
Come si può vedere dalla relazione che impone l’uguaglianza fra i moduli dei due campi elettrici:
E_1 = \frac{kQ_1}{(R_1)^2} = \frac{kQ_2}{(R_2)^2} = E_2
[/math]
questa relazione non dipende dalla costante
k = \frac{1}{4 π ε_0 ε_r }
[/math]
poiché si semplifica.
Il fatto che le due cariche siano immerse in un dielettrico influisce sull’intensità del campo che ciascuna carica crea.
Consideriamo la carica
Q_1
[/math]
ed il campo elettrico che essa genera in un punto P, distante R dalla carica stessa:
E = \frac{kQ}{(R)^2}
[/math]
Supponiamo che sia immersa in un dielettrico ε_r.
Vediamo che la costante k
k = \frac{1}{4 π ε_0 ε_r}
[/math]
assume un valore minore rispetto al valore che avrebbe se la carica Q fosse immersa nel vuoto, ossia nel caso in cui
ε_r =1
[/math]
avremmo
k’ = \frac{1}{4 π ε_0}
[/math]
con k’ > k
quindi il valore del campo elettrico E ottenuto in un punto P dello spazio in presenza di un dielettrico è minore del campo generato dalla stessa carica Q, ma immersa in un dielettrico.
Questo fenomeno si spiega poiché il dielettrico in presenza della carica (o delle cariche) si polarizza ed in seguito alla polarizzazione varia la forza di interazione fra le cariche (forza di Coulomb).
Tale forza essendo direttamente collegata alla definizione di campo elettrico, influisce sull’intensità dello stesso:
F_c = \frac{kQq}{(R)^2}
[/math]
q = carica esploratrice
E = \frac{F_c}{q}
[/math]
E = \frac{kQ}{(R)^2}
[/math]
In particolare, se F è la forza agente fra le due cariche
Q_1
[/math]
e
Q_2
[/math]
poste nel vuoto ad una data distanza L, ed
F_d
[/math]
è la forza con cui le stesse due cariche, alla stessa distanza, interagiscono in un mezzo isolante (ossia in presenza di dielettrico)
il rapporto
\frac{F}{F_d}
[/math]
descrive la costante
ε_r
[/math]
= costante dielettrica relativa del mezzo
ε_r = \frac{F}{F_d}
[/math]
.
E’ ovvio che se
F = F_d
[/math]
allora
ε_r = 1
[/math]
e si rientra nel caso in cui le cariche interagenti sono poste nel vuoto.
Per ulteriori approfondimenti su questo argomento vedi anche qua
Domande da interrogazione
- Qual è il valore della carica [math]Q_2[/math] nel problema?
- Il campo elettrico sarebbe nullo nel punto C se le cariche fossero immerse nel vuoto?
- Come si calcola il campo elettrico generato da una carica puntiforme?
- Cosa implica il Principio di Sovrapposizione degli Effetti nel contesto del campo elettrico?
- Come influisce un dielettrico sull'intensità del campo elettrico generato da una carica?
Il valore della carica [math]Q_2[/math] è [math]2,1•10^-2 C[/math].
Sì, il campo elettrico sarebbe ancora nullo nel punto C anche se le cariche fossero immerse nel vuoto, poiché la relazione di equilibrio non dipende dalla costante dielettrica del mezzo.
Il campo elettrico generato da una carica puntiforme è calcolato con la formula [math]E = \frac{kQ}{R^2}[/math], dove [math]k[/math] è la costante del mezzo, [math]Q[/math] è la carica, e [math]R[/math] è la distanza dal punto di interesse.
Il Principio di Sovrapposizione degli Effetti implica che i campi elettrici generati da più cariche si sommano vettorialmente, determinando il campo totale in un punto dello spazio.
Un dielettrico riduce l'intensità del campo elettrico generato da una carica, poiché la costante [math]k[/math] assume un valore minore rispetto a quando la carica è nel vuoto, a causa della polarizzazione del dielettrico.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
