Concetti Chiave
- Nel primo caso, con cariche identiche, il campo elettrico nel punto medio è nullo, poiché le forze si annullano reciprocamente.
- Nel secondo caso, le cariche sono diverse, generando forze di intensità differente nel punto medio.
- Le forze sono calcolate usando la legge di Coulomb, considerando una carica di prova di 1 C nel punto medio.
- La forza risultante è la somma vettoriale delle forze individuali, risultante in una forza totale di 0,9 x 1010 N.
- Il campo elettrico risultante ha un'intensità di 0,9 x 1010 N/C, con direzione lungo la retta che unisce le due cariche.
Nell'esercizio seguente, suddiviso in più punti andremo a studiare il campo elettrico in un punto preciso del piano studiando due diversi casi: il primo caso riguarderà una situazione in cui le due cariche sono identiche, nel secondo caso tratteremo un caso leggermente diverso, in cui le due cariche hanno valori distinti. Vediamo ora il testo dell'esercizio.
Testo dell'esercizio
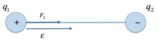
Due cariche puntiformi
e
si trovano nel vuoto a una distanza di
.
Qual è il vettore campo elettrico nel punto medio tra le posizioni occupate dalle cariche quando:
- [math]q_1 = q_2[/math]
-
[math]q_1 = 2,4 \cdot 10^{-3} C [/math]e[math] q_2 = - 1,2 \cdot 10^{-3} C [/math]
Svolgimento dell'esercizio
Per il primo punto, se
e
Di conseguenza, la forza risultante nel punto
è nulla, quindi è nullo anche il campo elettrico. Nel secondo caso, invece, le due cariche sono diverse; il punto medio, quindi, è soggetto a forze diverse:
Calcoliamo l'intensità di queste forze utilizzando la legge di Coulomb; consideriamo nel punto
una carica di prova di valore
:
La forza risultante è data dalla somma vettoriale delle due forze trovate:
Troviamo l'intensità del campo elettrico con la formula
:
Il vettore campo elettrico, poi, ha direzione giacente sulla retta che unisce le due cariche, e poiché la carica è positiva, il suo verso è lo stesso dei vettori forza.
Domande da interrogazione
- Cosa succede al campo elettrico nel punto medio quando le due cariche sono identiche?
- Come si calcola la forza risultante nel secondo caso, quando le cariche sono diverse?
- Qual è l'intensità del campo elettrico nel punto medio quando le cariche sono diverse?
Quando le due cariche sono identiche, le forze esercitate da ciascuna carica nel punto medio si annullano reciprocamente, rendendo il campo elettrico nullo.
La forza risultante si calcola sommando vettorialmente le forze esercitate dalle due cariche, utilizzando la legge di Coulomb per determinare l'intensità di ciascuna forza.
L'intensità del campo elettrico nel punto medio, quando le cariche sono diverse, è di \(0,9 \cdot 10^{10} N/C\), con direzione lungo la retta che unisce le due cariche e verso determinato dalla carica positiva.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
