Campo elettrico - Definizione e che cos'è

In questo appunti viene presentata la definizione di campo elettrico in ambito fisico. In fisica la nozione di campo elettrico è stata coniata da Michael Faraday per meglio fare comprendere l'interazione che sussiste tra delle cariche che si trovano a una determinata distanza l'una dall'altra. Vengono riportate anche le regole generali del campo elettrico e le formule corrispondenti.

Campo elettrico

Il campo elettrico è una grandezza fisica vettoriale che esprime le proprietà dello spazio dovute alla presenza in esso di una o più cariche.

Il concetto di campo elettrico venne introdotto da Michael Faraday per spiegare l’interazione tra cariche poste ad una certa distanza l’una dall’altra. La forza che si esercita tra due corpi carichi è una forza a distanza, come quella gravitazionale che si esercita tra due masse. In ognuno dei due casi non era ancora chiaro come un corpo che si trova in un punto A possa sentire l’effetto elettrico dovuto ad un secondo corpo che, invece, si trova in un punto B lontano. Proprio per questo motivo è stato introdotto il concetto di campo elettrico, costituito da due idee: 1) La presenza di una carica elettrica modifica lo spazio circostante e, in particolare, cambia le proprietà in un punto B in cui si trova la carica ; 2) Questa carica riesce ad avvertire una forza elettrica dovuta alle nuove proprietà dello spazio in cui si trova.
Si dice, così, che la carica genera un campo elettrico e che la zona di spazio in cui si possono avvertire forze elettriche è sede di un campo elettrico. Se noi mettessimo una carica positiva in un punto P, potremmo notare che la forza che agisce su dipende da tre fattori: 1) Cariche che formano il campo, perché se fossero diverse sarebbe diversa anche ; 2) Punto P, perché in un’altra zona la F-> potrebbe essere diversa; 3) Valore q+, perché se fosse più grande sarebbe più grande anche la .
Una carica di prova, infatti, è una carica elettrica abbastanza piccola da non modificare, a causa delle forze che esercita, il sistema.
Noi, però, vogliamo trovare una grandezza che descriva la forza elettrica in ogni punto dello spazio, senza dipendere dalla carica di prova che si prende in considerazione. Per questo motivo è stata introdotta una grandezza unitaria che si ottiene dividendo la per la . Questa nuova grandezza si chiama proprio vettore campo elettrico e si misura in Newton/Coulomb.
In sostanza, si mette la carica di prova in un punto, si osservano il verso e la direzione della forza e si misura con un dinamometro il valore della forza. Per quanto riguarda il verso e la direzione del campo elettrico, questi sono gli stessi della forza che agisce sulla carica di prova. Conoscendo il campo elettrico, possiamo calcolarci la forza che agisce su qualsiasi carica: basta moltiplicare per q i due membri che compongono la e isolare l’incognita .
Inoltre, se la carica q è positiva, il campo elettrico e la forza hanno lo stesso verso e stessa direzione; se la carica q è negativa, il campo elettrico e la forza hanno stessa direzione e verso opposto.

Proprietà e linee del campo elettrico

La forza che si esercita tra due corpi carichi è una forza a distanza che si ottiene senza un contatto materiale tra i due corpi. Tuttavia un corpo fa sentire la sua forza a un altro, anche se è molto lontano e se lo spazio che li divide è molto. Immaginiamo di avere un corpo A sulla terra carico e un corpo B su un pianeta molto lontano. Se annulliamo la carica di A, istantaneamente, si dovrebbe annullare quella di B, ma ciò non accade. Diciamo che quando un corpo A viene caricato in tutto lo spazio circostante si genera una situazione nuova poiché diventa sede di cariche elettriche. Invece il corpo B che si trova in un punto dello spazio risente delle cariche elettriche generate da A.
Si dice che una regione di spazio è sede di un corpo elettrico quando un corpo che si trova in un punto qualsiasi dello spazio è soggetto a forze elettriche. Il corpo C viene definito corpo di prova (deve essere piccolo per permettere la misura del campo in ogni punto).
Il campo elettrico generato dalla carica (QA) esiste indipendentemente che in un punto (P) si trovi un corpo carico. La forza che agisce sul corpo è dovuta al campo elettrico e non a una diretta azione a distanza del corpo A. Naturalmente se in uno spazio vi sono più cariche (A1, A2, A3,…) esse generano in tutto lo spazio circostante, un campo elettrico.

Le proprietà del campo elettrico sono descritte in ogni punto dello spazio con un vettore campo elettrico E ⃗. Mettiamo in un punto P una carica positiva +q di prova. Il vettore campo elettrico E ⃗ nel punto P è definito come il rapporto tra la forza elettrica che subisce la carica di prova posta in quel punto e la carica stessa.
E ⃗≡ F ⃗/(+q)
Nel sistema internazionale si misura in N/C. Essa non dipende dal valore della carica di prova di cui ci serviamo per misurarla.
Se usassimo una carica di prova doppia o tripla otterremo sempre lo stesso vettore campo elettrico, perché la forza sarebbe doppia o tripla. Il campo elettrico generato da una sola carica Q può essere sia positivo che negativo. La forza che essa esercita sulla carica di prova +q possa a distanza R è uguale a F= 1/4πε ∙ (Q q)/R^2 quindi la forza di Coulomb è direttamente proporzionale al valore della carica di prova. Per l’intensità del campo elettrico E si ottiene E= F/q= (1/4πε ∙ (Q q)/R^2 )/q=1/4πε ∙ Q/R^2
Se le cariche sono poste nel vuoto si ha che ε= ε_0 e quindi è uguale 1/4πε0 ∙ Q/R^2
La carica di prova q non compare in quest’espressione poiché è stata semplificata in quanto compariva sia al numeratore che al denominatore. La direzione E ⃗ è la stessa di F ⃗perché si deve dividere quest’ultimo per il numero positivo +q.
Se il campo è generato da più di una carica, ad esempio Q1 e Q2, la forza F ⃗ sulla carica di prova +q è uguale alla somma vettoriale della forza (F_1 ) ⃗ e (F_2 ) ⃗ che le singole cariche esercitano separatamente su più q: F ⃗= (F_1 ) ⃗+ (F_2 ) ⃗
Il campo elettrico E ⃗ è il vettore risultante dalla somma dei campi elettrici E1 e E2 che sono generati rispettivamente dalle carica Q1 e Q2. Il campo elettrico dipende soltanto dalle cariche che lo generano e dal punto in cui è misurato. L’intensità del campo elettrico in un punto è numericamente uguale all’intensità della forza che si eserciterebbe sull’unità di carica posta in quel punto.
F ⃗=q E ⃗
Conoscendo il vettore E ⃗ in un punto P possiamo calcolare la forza che agisce su qualsiasi carica posta in quel punto.
Se questa carica è positiva la forza ha direzione e verso uguali a quelli del campo elettrico.
Se invece la carica è negativa, la direzione della forza è uguale a quella di E ⃗, ma il verso è opposto.
Il campo elettrico è un esempio di campo vettoriale. Esistono anche campi scalari in cui ad ogni punto di una zona di spazio si associa un numero.

Le linee di campo: Per visualizzare il campo elettrico generato da più cariche possiamo tracciare una serie di vettori in più punti nello spazio. Devono avere direzione e verso uguale al campo elettrico e lunghezza proporzionale all’intensità. Tuttavia se E ⃗ è disegnato in pochi punti, essa risulta grossolana, se invece E ⃗ è disegnato in più punti, diventa confusionaria. Per questo motivo si usano le linee di campo.
Spostando di piccoli tratti la carica nella direzione e nel verso della forza elettrica si formerà una spezzata.
Più gli intervalli sono fitti più si formerà una linea di campo.
Essa consente di individuare la direzione e il verso del vettore campo elettrico. Per ogni punto di campo si può tracciare solo una linea di campo. Esse escono dal punto se la carica che le genera è positiva, viceversa se è negativa.

Campo elettrico, analisi

Tutte le caratteristiche di un campo elettrico vengono descritte in maniera quantitativa.
In esso viene identificato un "vettore campo elettrico" col simbolo:

Ipotizziamo di posizionare in un qualsiasi punto A del campo elettrico una carica positiva +t e proviamo a misurare, utilizzando un dinamometro, la forza

che agisce su di essa. Successivamente dividiamo il vettore per carica +t.
Il vettore campo elettrico , nel punto A, viene espresso come il rapporto tra la forza elettrica che agisce sulla carica di prova +t e la carica +t stessa. Perciò, possiamo definirlo con la formula:
Se dovessimo utilizzare una carica di prova doppia, per esempio, il vettore campo elettrico ottenuto sarebbe identico, poiché la forza sarebbe proporzionale e quindi, in questo caso, doppia anch'essa.

Nel Sistema Internazionale, l'unità di misura del campo elettrico è il :

dove N sta per Newton, e C sta per Coulomb.

Proviamo invece a considerare un campo elettrico costituito da un'unica carica T, generica.
Per la legge di Coulomb, sappiamo che la forza che questa carica esercita su quella di prova +t, messa ad una certa distanza s è equivalente a:

Dalla quale otteniamo:

Se le cariche si trovano in uno spazio "vuoto" (o nel vuoto), si avrà:

La direzione di

sarà dunque la stessa di per la carica +t, mentre notiamo che è stata semplificata la carica t in quanto presente sia al numeratore, che al denominatore.

Rappresentazione del campo elettrico

Vediamo alcuni campi elettrici rappresentati attraverso le linee di forza.
1. Campo elettrico generato da una carica puntiforme positiva.

Troviamo una disposizione a raggiera delle linee di forza, e i raggi sono simmetrici perché tutte le direzioni sono equiprobabili.
2. Campo elettrico generato da una carica puntiforme negativa.

3. Campo elettrico generato da due cariche perfettamente uguali.

La risultante del campo elettrico è tangente alla linea di forza in ogni suo punto.
F_2 Minore è la distanza, Maggiore sarà la Forza elettrica.
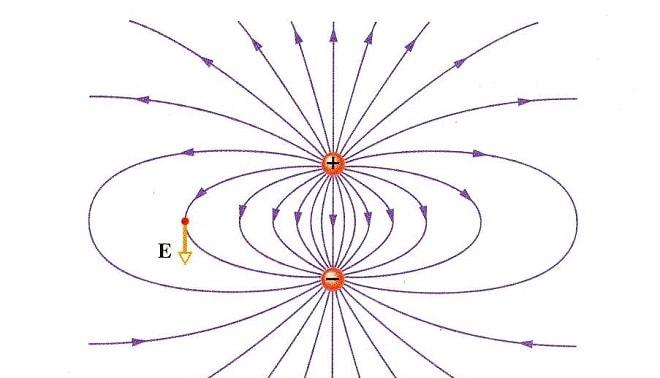
4. Campo elettrico generato da un Dipolo elettrico.

Un dipolo elettrico è un sistema costituito da due cariche puntiformi che hanno uguale carica, ma di segno opposto.
5. Campo elettrico generato da una lastra metallica infinitamente estesa.

Considerando il campo elettrico al centro della lastra, noteremo che le linee di forza sono equidistanti e parallele; agli estremi le linee di forza si comporteranno come per una carica puntiforme.
6. Campo generato in un condensatore piano.

Un condensatore piano è formato da un sistema di due lastre infinitamente estese che possiedono la stessa quantità di carica, ma di segno opposto.
La distanza tra le due lastre è molto piccola, tanto che d_2 è quasi uguale a d_1: ciò comporta che q_0 subisce una forza attrattiva pari a quella repulsiva.
Inoltre, all’esterno del condensatore il campo elettrico sarà nullo perché i campi elettrici delle due lastre, avendo verso opposto e uguale intensità, si annulleranno a vicenda.
7. Campo generato da un filo infinitamente esteso rettilineo carico positivamente.

Le linee di forza sono perpendicolari al filo in ogni punto; sono uscenti dal filo (perché il filo è carico positivamente; se fosse stato negativo, le linee sarebbero state entranti); il campo elettrico è sempre costante.
8. Campo generato da una sfera conduttrice carica.
La sfera si comporterà come una carica puntiforme, come se tutta la carica fosse concentrata nel centro della sfera, con un campo elettrico:
- diretto radialmente, ovvero, presenta una simmetria sferica;
- Ha un’intensità uguale in tutti i punti equidistanti dal centro della sfera;
- Ha verso uscente se si considera una sfera carica positivamente.

Campo elettrico, descrizione

La forza che si esercita tra due corpi carichi è una forza a distanza.Non vi è connessione materiale tra i due corpi che interagiscono.
L’esistenza di forze di questo tipo suscita qualche perplessità.Questa difficoltà può essere superata,quando un corpo A viene caricato,si genera in tutto lo spazio circostante una situazione nuova,diversa da quella che esisteva in precedenza;lo spazio diventa sede di forze elettriche.Un altro corpo carico B,messo in qualche punto dello spazio,comincia a “sentire”una orza elettrica di cui A è la causa.
Il corpo che carichiamo è chiamato corpo di prova.
Il campo elettrico esiste indipendentemente dal fatto che in P si trovi un corpo carico.
A ogni punto dello spazio possiamo associare il vettore campo elettrico.Il vettore campo elettrico misura quantitativamente li effetti elettrici.Mettiamo in un punto P una carica positiva +q e misuriamo con un dinamometro la forza F che essa subisce.Poi dividiamo il vettore F per la quantità di carica +q.
Il vettore campo elettrico E nel punto P è definito come il rapporto tra la forza elettrica che subisce la carica di prova posta in quel punto e la carica stessa.
Nel Sistema Internazionale il campo elettrico si misura in Newton/Coulomb.
Se il campo è generato da più di una carica,per esempio da Q1 e Q2, la forza F sulla carica di prova +q è uguale alla somma vettoriale delle forze F1 e F2 che le singole cariche esercitano separatamente su +q.
Il vettore è risultante dalla somma dei campi elettrici E1 e E2,che sono generati rispettivamente dalle cariche Q1 e Q2. E1 e E2 sono indipendenti dal valore della carica di prova,dipende soltanto dalle cariche che lo generano e dal punto in cui è misurato.
Una volta che conosciamo E siamo in grado di calcolare la forza che il campo esercita su qualsiasi carica,basta moltiplicare il vettore E per il valore della carica q.La direzione della forza è la stessa di quella del campo.Se la carica è positiva,anche il verso è lo stesso.Se invece è negativa,il verso è contrario a quello della forza.
Il campo elettrico è un esempio di campo vettoriale,in cui a ogni punto di una zona di spaziosi associa uno e un solo vettore.
Il flusso del campo elettrico vi è quando si ha una superficie S piana e un campo elettrico E costante,se la superficie non è piana oppure il campo elettrico non è costante,per calcolare il flusso del campo elettrico occorre suddividere la superficie in parti così piccole da soddisfare le condizioni (superficie piana e campo elettrico costante),calcolare il flusso attraverso tali parti con la formula e poi sommare i risultati parziali ottenuti.
Determiniamo ora il flusso del campo elettrico,generato da una carica puntiforme Q,attraverso una superficie sferica E,di raggio r e area S,che ha il centro coincidente con la carica.Abbiamo scelto una superficie sferica perché il campo elettrico della carica ha la stessa intensità E in tutti i punti.
Suddividiamo la superficie in n parti piane,ciascun vettore diretto lungo il raggio è rivolto verso l’esterno della sfera,è parallelo al vettore E1.
Il flusso del campo elettrico è la somma dei flussi parziali.Il flusso è il prodotto dell’intensità E del campo per la somma delle aree delle piccole superficie.Tale somma è uguale all’area della superficie S della sfera.
Il flusso attraverso la sfera è proporzionale alla carica Q e non dipende dal raggio della sfera.
Se il punto passa dal punto B al punto A sotto l’azione di una forza conservativa F,si definisce la differenza di energia potenziale dove W ab è il lavoro fatto dalla forza F nel passaggio da A a B.
Una volta scelta una condizione di zero si chiama energia potenziale in un punto B la differenza di energia potenziale tra B e R.
L’energia potenziale elettrica di due cariche puntiformi a distanza r si avrà quando scelta una condizione di o anche la costante risulterà o.
Se spostiamo q dal punto A al punto B,possiamo determinare la differenza di energia potenziale tra la condizione iniziale e quella finale.
A partire dalla differenza di energia potenziale elettrica (che dipende dalla carica di prova) definiremo una nuova grandezza,la differenza di potenziale elettrico,che non dipende dalla carica di prova,ma soltanto dalle N cariche che generano il campo e dai punti tra cui la si calcola.
L’unità di misura del potenziale elettrico è il volt.
Con la scelta di porre uguale a o il potenziale elettrico nei punti infinitamente lontani,il potenziale elettrico sarà uguale a:

In ogni punto le linee di campo elettrico,sono perpendicolari alle superfici equipotenziali.
Si chiama superficie equipotenziale il luogo dei punti dello spazio in cui il potenziale elettrico assume un dato valore costante (sempre uguale).
Con la scelta più comune,di porre uguale a zero il potenziale nei punti infinitamente lontani,il potenziale elettrico del campo generato da una carica puntiforme Q,in un punto A che dista r da Q.

Autori che hanno contribuito al presente documento: robertamagnotta, ciocino91, daddy8, salvatoretkc, peor.