Goniometria: le formule del seno e del coseno

In quest'appunto troverai le definizioni e le formule principali della goniometria, con un focus sul concetto di seno e coseno.

Che cos'è la goniometria e come convertire l'ampiezza di un angolo in radianti

La goniometria è la branca della matematica che si occupa della misura degli angoli.

La trigonometria si occupa invece delle relazioni che legano le misure dei lati di un triangolo a quelle dei suoi angoli. Un angolo è una parte di piano compresa tra due semirette aventi la stessa origine.

L'origine prende il nome di vertice dell'angolo. L'unità di misura degli angoli usata abitualmente è il grado (indicato con

), definito come la 360esima parte dell'angolo giro. Per le applicazioni scientifiche viene utilizzata anche un'altra unità di misura detta radiante.

Si chiama angolo Radiante (

), l'angolo al centro di una circonferenza di raggio arbitrario che sottende un arco di lunghezza uguale al raggio stesso.
L'ampiezza

di un angolo espressa in radianti si calcola dividendo la lunghezza dell'arco corrispondente

per il raggio

:

ampiezza di un angolo in radianti = lunghezza dell'arco / r, ossia

.
Quindi l'angolo giro, che sottende l'intera circonferenza in radianti sarà:

, ossia

. Per quanto riguarda gli altri angoli, invece, abbiamo che l'angolo piatto misura

cioè

mentre l'angolo retto misura

, cioè

.

Per esprimere l'ampiezza di un angolo dato in gradi, nell'unità radianti o viceversa si utilizza la seguente proporzione:

, in cui

è l'ampiezza dell'angolo in gradi mentre

è l'ampiezza dell'angolo in gradianti.

Cosa sono gli angoli orientati e la circonferenza goniometrica

Si può inoltre considerare l'angolo da due diversi punti di vista:

• in modo statico, come quella parte di piano compresa tra due semirette aventi la stessa origine
• in modo dinamico, come la parte di piano descritta dalla rotazione che compie una semiretta attorno alla sua origine a partire da una posizione iniziale

Un angolo si dice orientato quando viene segnato come lato iniziale uno dei due lati ed è stabilito un verso di rotazione. Solitamente viene assegnato il segno positivo al verso antiorario e il segno negativo a quello orario.

Introducendo nel piano un sistema di riferimento cartesiano, consideriamo un angolo in posizione normale quando il suo vertice coincide con l'origine, il suo lato iniziale coincide con il semiasse positivo delle ascisse

e si assume come positivo il verso antiorario.
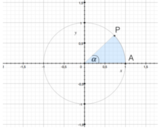
Si chiama circonferenza goniometria una circonferenza con centro nell'origine e raggio unitario.

Considerata

l'ampiezza di un angolo in posizione normale, espressa in radianti è un qualunque numero reale.

è il punto in cui, il lato finale dell'angolo di ampiezza

, interseca con la circonferenza goniometrica.

L'ascissa e l'ordinata del punto

variano in funzione di

. Verrà indicato con

l'ascissa del punto

e con

l'ordinata del punto

.

Sia l'ascissa sia l'ordinata del punto

variano da

a

, perché

appartiene alla circonferenza goniometrica.
Quindi:

e

I teoremi sul seno e sul coseno

Esiste una relazione fondamentale che lega seno e coseno e vale per qualsiasi valore di

, ossia

. Dalla relazione fondamentale tra seno e coseno è possibile ricavare altre due formule:

Casi legati ad angoli dalle ampiezze particolari

Angoli il cui lato finale coincide con uno dei semiassi

Quando l'ampiezza dell'angolo è un multiplo di

(angolo retto), il lato finale dell'angolo coincide con il uno dei semiassi. In tali casi uno tra il seno e coseno è uguale a

, mentre l'altro valore è

oppure

.

In particolare:

• se l'ampiezza è
  [math]0°[/math]
  , il coseno dell'angolo è
  [math]1[/math]
  mentre il seno è
  [math]0[/math]
• se l'ampiezza è
  [math]\frac{\pi}{2}[/math]
  , il coseno dell'angolo è
  [math]0[/math]
  mentre il seno è
  [math]1[/math]
• se l'ampiezza è
  [math]\pi[/math]
  , il coseno dell'angolo è
  [math]-1[/math]
  mentre il seno è
  [math]0[/math]
• se l'ampiezza è
  [math]\frac{3\pi}{2}[/math]
  , il coseno dell'angolo è
  [math]0[/math]
  mentre il seno è
  [math]-1[/math]

Angoli che danno luogo ad un triangolo rettangolo isoscele

Quando l'ampiezza dell'angolo è multipla di

(ma non di

), si viene a determinare un triangolo isoscele, di ipotenusa unitaria. Da ciò si deduce che i due cateti essendo uguali misurano entrambi

, mentre il seno e il coseno, in valore assoluto, sono

.

Si ha, inoltre, che:

• se l'ampiezza è
  [math]\frac{\pi}{4}[/math]
  , il coseno e il seno dell'angolo sono
  [math]\frac{\sqrt2}{2}[/math]
• se l'ampiezza è
  [math]\frac{3\pi}{4}[/math]
  , il coseno dell'angolo è
  [math]-\frac{\sqrt2}{2}[/math]
  mentre il seno è
  [math]\frac{\sqrt2}{2}[/math]
• se l'ampiezza è
  [math]\frac{5\pi}{4}[/math]
  , il coseno dell'angolo è
  [math]-\frac{\sqrt2}{2}[/math]
  mentre il seno è
  [math]-\frac{\sqrt2}{2}[/math]
• se l'ampiezza è
  [math]\frac{7\pi}{4}[/math]
  , il coseno dell'angolo è
  [math]\frac{\sqrt2}{2}[/math]
  mentre il seno è
  [math]-\frac{\sqrt2}{2}[/math]

Angoli che danno luogo a un triangolo rettangolo 30-60-90

Quando l'ampiezza dell'angolo è multipla di

(ma non di

), si viene a determinare un triangolo rettangolo di angoli

.
Il cateto opposto all'angolo di

misura

, mentre il cateto opposto all'angolo di

cioè

misura

.
In valore assoluto

e

sono i valori di seno e coseno di tali angoli.

Per ulteriori approfondimenti su seno e coseno vedi anche qui