In questo appunto di matematica si tratta il piano cartesiano, come è stato ideato, come si costruisce ed il suo utilizzo nello studio della geometria.
Indice
Cenni storici: Cartesio e l’Algebra Geometrica
Dal punto di vista storico, l’Algebra e la Geometria si presentano come due discipline nettamente separate, ciascuna delle quali si svolge indipendentemente dall’altra, con procedimenti propri. Un sussidio ci calcolo è tuttavia necessario per la Geometria quando questa deve affrontare il problema delle misurazioni, ossia dove nascono le prime relazioni tra la scienza dell’estensione e quella del numero. Inoltre, la geometria elementare usa dei procedimenti non perfettamente adattabili allo studio di problemi geometrici di carattere complesso. In base a queste necessità si è pensato di tradurre tali problemi geometrici in problemi algebrici.Il maggior merito di tale concezione è dovuto a due grandi matematici come P. Fermat (1601 – 1663) e ad R. Descartes, comunemente conosciuto come Cartesio (1596 -1650). Soprattutto quest’ultimo è stato colui che ha posto le basi della moderna Geometria Analitica, inizialmente chiamata Algebra Geometrica:
Cartesio ha dato un metodo generale per la soluzione di tutti i problemi di geometria e, a tal fine, si basa su due concetti fondamentali:
- il metodo delle coordinate;
- la rappresentazione, tramite il metodo delle coordinate, di qualsiasi equazione algebrica in due incognite, come curva del piano.
Tramite le coordinate cartesiane si possono individuare i punti nel piano mediante due valori numerici (ascissa ed ordinata) oppure nello spazio mediante tre valori (ascissa, ordinata ed elevazione). Il metodo cartesiano, soprattutto, portò grandi vantaggi in quanto gli enti geometrici vengono considerati luoghi geometrici, ossia insiemi di punti che godono di specifiche proprietà le quali vengono tradotte in termini matematici attraverso equazioni che descrivono l’entità geometrica: sia crea una corrispondenza biunivoca tra l’entità geometrica e l’espressione algebrica.
Al sistema di coordinate cartesiane ne sono stati affiancati altri come:
- sistema delle coordinate polari;
- sistema delle coordinate geografiche;
- ecc.
Il piano cartesiano
Si consideri una retta r, diremo che su di essa è stato fissato un sistema di ascisse nel caso in cui siano stati fissati:- una orientazione della retta;
- un punto O, appartenente alla retta stessa, e chiamato origine;
- un segmento u, da assumersi come unitario.
chiameremo ascissa di un punto P della retta r, il numero reale
[math]
x_P
[/math]
che ha per modulo la misura del segmento x_P
[/math]
[math]
\bar{OP}
[/math]
, rispetto all’unità di misura u prescelta ed il cui segno è positivo o negativo a seconda che P segue o preceda O rispetto all’orientazione della retta. L’ascissa nel punto O è zero.\bar{OP}
[/math]
Ad ogni punto P di r corrisponde uno ed un solo numero reale,
[math]
x_P
[/math]
, ossia una ed una sola ascissa di P (P risulta univocamente determinato). x_P
[/math]
In definitiva si ha che: fissando su di una retta r un sistema di ascisse si stabilisce una corrispondenza biunivoca fra l’insieme dei punti della retta i l’insieme dei numeri reali
[math]
\mathbb{R}.
[/math]
\mathbb{R}.
[/math]
Considerato un piano
[math]
\pi
[/math]
diremo che su tale piano è fissato un sistema di coordinate cartesiane ortogonali, nel caso in cui su \pi
[/math]
[math]
\pi
[/math]
sono state fissate due rette orientate (o assi) x ed y fra loro perpendicolari, su ciascuna delle quali è stato fissato un sistema di ascisse tale che il punto comune alle due rette sia assunto come loro origine comune, O, ed il segmento unitario u sia il medesimo per entrambe le rette.\pi
[/math]
Le ascisse dei punti dell’asse y verranno chiamate ordinate, mentre quelle dei punti sull’asse x sono le ascisse. Conseguentemente, gli assi x ed y vengono chiamati, rispettivamente, asse delle ascisse ed asse delle ordinate. Si dice anche che x ed y costituiscono gli assi cartesiani ed il piano xy (
[math]
\pi
[/math]
, individuato da queste due rette) prende il nome di piano cartesiano.\pi
[/math]
Le coordinate cartesiane
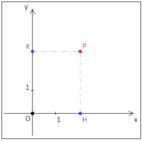
Si consideri un punto P del piano cartesiano[math]
\pi
[/math]
e da esso si conduca la retta parallela all’asse y che incontra l’asse x nel punto \pi
[/math]
[math]
P_x
[/math]
, e la parallela all’asse x che incontra l’asse y nel punto P_x
[/math]
[math]
P_y:
[/math]
P_y:
[/math]
ai punti
[math]
P_x
[/math]
e P_x
[/math]
[math]
P_y
[/math]
sono associati due numeri reali, rispettivamente, P_y
[/math]
[math]
x_P
[/math]
e x_P
[/math]
[math]
y_P
[/math]
che vengono chiamati ascissa ed ordinata del punto P. Tali numeri, presi nell’ordine precedentemente scritto, costituiscono le coordinate cartesiane del punto P:y_P
[/math]
[math]
P = (x_P; y_P).
[/math]
P = (x_P; y_P).
[/math]
In modo del tutto analogo si vede che ad ogni coppia di numeri reali,
[math]
(x_P; y_P)
[/math]
, corrisponde uno ed un solo punto P del piano (x_P; y_P)
[/math]
[math]
\pi
[/math]
: \pi
[/math]
tracciando la parallela all’asse y per il punto
[math]
x_P
[/math]
e la parallela all’asse x per x_P
[/math]
[math]
y_P
[/math]
, queste si incontrano unicamente in P (unico punto in comune).y_P
[/math]
In base alle precedenti considerazioni si può concludere che:
dato un piano
[math]
\pi
[/math]
e fissato su di esso un sistema o un riferimento di coordinate cartesiane ortogonali si viene a stabilire una corrispondenza biunivoca fra i punto del piano ed il prodotto cartesiano \pi
[/math]
[math]
\mathbb{R} X \mathbb{R}.
[/math]
\mathbb{R} X \mathbb{R}.
[/math]
Gli assi cartesiani x ed y, suddividono il piano cartesiano xy (
[math]
\pi
[/math]
) in quattro parti ciascuna delle quali è chiamata quadrante. \pi
[/math]
In base alla convenzione standard, in cui l’asse delle x viene fissato orizzontale e positivo verso destra (ossia fissando i valori delle x crescenti da sinistra verso destra, senso di lettura europeo) mentre l’asse y viene fissato verticale (perpendicolare all’asse x) e positivo dal basso verso l’alto (le y sono crescenti dal basso verso l’alto), i quattro quadranti vengono classificati come:
- I quadrante, [math]0 e
x_P >
[/math][math]
y_P > 0;
[/math] - II quadrante, [math]e
x_P [/math][math]
y_P > 0;
[/math] - III quadrante, [math]e
x_P [/math][math]
y_P [/math] - IV quadrante, [math]e
x_P > 0
[/math][math]
y_P [/math]
Prime applicazioni di Geometria Analitica: distanza fra due punti.
Fissato un sistema di riferimento cartesiano ortogonale di origine O, si individuano i punti[math]
P_1
[/math]
e P_1
[/math]
[math]
P_2
[/math]
tramite le loro coordinate cartesiane:P_2
[/math]
[math]
P_1 = (x_1, y_1)
[/math]
P_1 = (x_1, y_1)
[/math]
[math]
P_2 = (x_2, y_2).
[/math]
P_2 = (x_2, y_2).
[/math]
Si vuole determinare la distanza in valore assoluto
[math]
d = \bar{P_1P_2}
[/math]
di tali punti tramite le loro coordinate.d = \bar{P_1P_2}
[/math]
Siano
[math]
A_1
[/math]
ed A_1
[/math]
[math]
A_2
[/math]
le proiezioni ortogonali di A_2
[/math]
[math]
P_1
[/math]
e P_1
[/math]
[math]
P_2
[/math]
sull’asse delle x e P_2
[/math]
[math]
B_1
[/math]
e B_1
[/math]
[math]
B_2
[/math]
le proiezioni ortogonale di B_2
[/math]
[math]
P_1
[/math]
e P_1
[/math]
[math]
P_2
[/math]
sull’asse delle y, si ha che:P_2
[/math]
[math]
\bar{OA_1} = x_1
[/math]
\bar{OA_1} = x_1
[/math]
[math]
\bar{OA_2} = x_2
[/math]
\bar{OA_2} = x_2
[/math]
[math]
\bar{OB_1} = y_1
[/math]
\bar{OB_1} = y_1
[/math]
[math]
\bar{OB_2} = y_2.
[/math]
\bar{OB_2} = y_2.
[/math]
Utilizzando le precedenti espressioni si può calcolare:
[math]
\bar{A_1A_2} = x_2 - x_1
[/math]
\bar{A_1A_2} = x_2 - x_1
[/math]
[math]
\bar{B_1B_2} = y_2 - y_1
[/math]
\bar{B_1B_2} = y_2 - y_1
[/math]
e applicando il Teorema di Pitagora al triangolo rettangolo individuato da tali segmenti si ottiene che
[math]
d^2 = (\bar{P_1P_2})^2b = (x_2 - x_1)^2 + (y_2 - y_1)^2
[/math]
d^2 = (\bar{P_1P_2})^2b = (x_2 - x_1)^2 + (y_2 - y_1)^2
[/math]
ossia si arriva alla seguente formula
[math]
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
[/math]
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
[/math]
la quale esprime la distanza fra due punti del piano in base alle loro coordinate cartesiane.
La retta che contiene il segmento che unisce i punti
[math]
P_1
[/math]
e P_1
[/math]
[math]
P_2
[/math]
è una funzione lineare espressa dall’equazione seguente:P_2
[/math]
[math]
\frac{y – y_1}{y_2 – y_1} = \frac{x – x_1}{x_2 – x_1}.
[/math]
\frac{y – y_1}{y_2 – y_1} = \frac{x – x_1}{x_2 – x_1}.
[/math]
Si vede che vi è una corrispondenza biunivoca tra i punti P della retta rappresentata dalla precedente equazione e le soluzioni della sua equazione cartesiana.
per ulteriori approfondimenti sul piano cartesiano veid anche qua
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
