Triangoli equilateri: proprietà e applicazioni sul piano cartesiano

In quest'appunto sono presenti delle informazioni generali sui triangoli equilateri, con un focus relativo alla verifica della condizione di esistenza di tale tipologia di triangolo mediante l'impiego del piano cartesiano.

Cosa studia la geometria analitica e perché è importante

La geometria analitica è la parte della matematica che studia le proprietà delle figure geometriche e degli enti fondamentali attraverso l'ausilio del piano cartesiano.

Ciò permette di quantificare le lunghezze sfruttando una proprietà dei punti su tale sistema di riferimento, ossia l'esistenza delle coordinate.

Queste ultime possono essere utilizzate, ad esempio, per il calcolo della distanza tra due punti attraverso l'utilizzo della formula

dove

sono rispettivamente le coordinate di due punti:

e

.

Le coordinate possono anche essere utilizzate per sancire l'equazione di una retta, cioè per descrivere in maniera analitica il luogo dei punti infinito aventi tutti la stessa direzione. Per sancire l'equazione di una retta, deve essere presente una delle seguenti due condizioni:

• devono essere noti due punti della retta (perché tra due punti passa una e una sola retta)
• deve essere noto un punto della retta e il coefficiente angolare

.

Nel primo caso, la formula da utilizzare è la seguente

mentre nel secondo caso bisogna far riferimento a quest'altra espressione

. In entrambe le formule

sono rispettivamente le coordinate dei punti

e

mentre

è il coefficiente angolare della retta.

I triangoli: cosa sono e le principali proprietà

I triangoli sono dei poligoni aventi tre lati e tre angoli. Essi possono essere riarrangiati in sottogruppi sfruttando le proprietà relative a questi ultimi elementi.
Per quanto riguarda i lati, i triangoli possono suddividersi in:

• triangolo scaleno, se dispone di tre lati e tre angoli disuguali
• triangolo equilatero, se presenta tre lati e tre angoli uguali
• triangolo isoscele, se dispone di due lati e due angoli alla base congruenti

guardando gli angoli, invece, sono distinguibili in:

• triangoli acutangoli, se presentano tutti gli angoli acuti
• triangoli ottusangoli, qualora sia presente un angolo ottuso
• triangoli rettangoli, se dispongono di un angolo retto

.

I triangoli presentano alcune proprietà generali relative alla somma dei lati e degli angoli. In particolare, la somma di tutti gli angoli interni corrisponde a un angolo piatto (

) mentre la somma di due lati è sempre inferiore alla lunghezza del terzo lato.

I triangolo equilateri: come verificare se un triangolo è equilatero nel piano cartesiano

Svolgiamo insieme un problema di geometria piana con l'aiuto della geometria analitica, usando il piano cartesiano. Ecco il testo del problema:

Verificare se il triangolo che ha per vertici

è equilatero. Calcolarne poi il perimetro.
Un triangolo equilatero ha tre lati congruenti e quindi tre angoli congruenti ciascuno di

. Come procediamo?

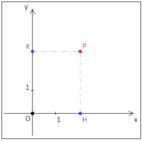
Nel piano cartesiano andiamo a rappresentare correttamente i tre punti che sono i vertici del nostro triangolo. Osservando la figura ci accorgiamo, subito che i tre lati non sono congruenti, ma facciamo una verifica analitica.
Partiamo dal lato orizzontale, quello di estremi

.

I punti hanno la stessa ordinata,

, basta fare la differenza tra le due ascisse per avere la misura del segmento. Usiamo il valore assoluto perché dobbiamo calcolare la misura di una lunghezza, e quindi non può essere negativa. Non dimentichiamo di fissare un'unità di misura, sia questa

, che poi può corrispondere ad esempio

Per valutare la misura del lato

usiamo la formula completa per la misura della distanza tra due punti nel piano cartesiano

Essendo questo lato diverso da

, possiamo già affermare che non è equilatero. Procediamo allora al calcolo della misura di

.

Per misurare

riutilizziamo la formula:

Non ci resta che sommare le misure dei tre lati per ottenere il perimetro:

=

. Se svolgiamo le radici quadrate e approssimiamo all’intero:

ovvero circa

.

Per ulteriori approfondimenti sui triangoli equilateri vedi anche qui