di 
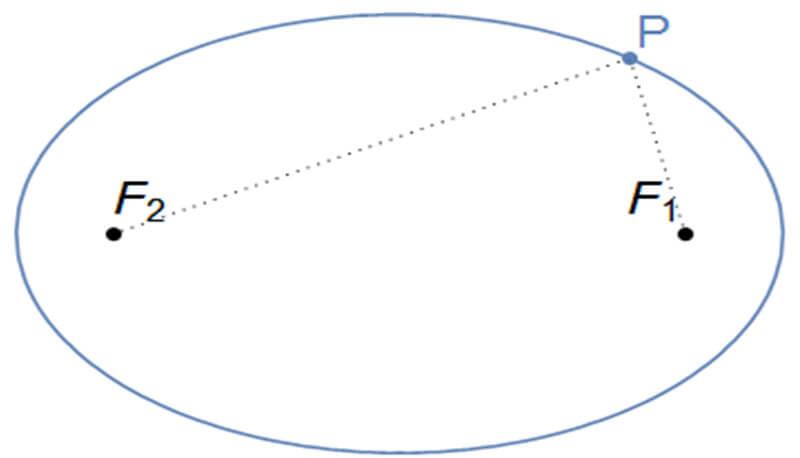
Definizione di ellisse
Si definisce ellisse la curva piana e chiusa che consiste di tutti i punti del piano tali che la somma delle loro distanze da due punti fissi (chiamati fuochi e posizionati in corrispondenza dell'asse maggiore) sia costante. Tale somma è pari alla lunghezza dell'asse maggiore dell'ellisse.
L'ellisse è la principale tra le sezioni coniche, cioè tra quelle sezioni che si ottengono intersecando tutte le generatrici di un cono con un piano obliquo al suo asse, ed è tale da presentare una doppia simmetria rispetto a due assi ortogonali. Può essere considerata come la deformata proiettiva di un cerchio, e su questa sua caratteristica si basano molte delle tecniche di tracciamento dell'ellisse utilizzate nel disegno tecnico (come ad esempio la cosiddetta "costruzione per otto punti").
Se indichiamo con 2a la lunghezza dell'asse maggiore, possiamo concludere che i punti di coordinate (a,0) e (-a,0) sono quelli in cui l'ellisse interseca l'asse orizzontale (asse x) del piano cartesiano, chiamati anche vertici orizzontali dell'ellisse. Diremo inoltre che a è lunghezza del semiasse maggiore.
L'asse maggiore è la retta che contiene i due fuochi dell'ellisse, ed è anche uno dei suoi assi di simmetria. L'ellisse ha anche un secondo asse di simmetria: è la retta che passa per il centro dell'ellisse ed è perpendicolare all'asse maggiore. Questo secondo asse è chiamato asse minore. Asse minore e asse maggiore sono detti assi principali dell'ellisse.
A meno che l'ellisse non sia traslata rispetto all'origine, normalmente il suo centro (e quindi il punto dove asse maggiore e asse minore si intersecano) coincide con l'origine degli assi cartesiani. Più in generale, definiremo il centro dell'ellisse come il punto medio tra i due fuochi, e più avanti vedremo come comportarci nel caso in cui non coincida con l'origine degli assi.
Indichiamo con (-c,0) e (c,0) le generiche coordinate dei due fuochi sull'asse maggiore.
Se indichiamo con (0,b) e (0,-b) le coordinate dei punti in cui l'ellisse interseca l'asse verticale (asse y) del piano cartesiano (tali che b < a), data la definizione di ellisse possiamo scrivere che:
Diremo inoltre che b è la lunghezza del semiasse minore e chiameremo i punti di coordinate (0,b) e (0,-b) vertici verticali dell'ellisse.
La formula inversa a quella che abbiamo appena scritto (e cioè:
Fatta questa premessa, ci proponiamo adesso di trovare l'equazione dell'ellisse, conoscendo le coordinate dei due fuochi (-c,0) e (c,0), e sapendo che la somma delle distanze di ogni punto P (x,y) dell'ellisse da questi due fuochi è costante e pari a 2a.
Ricordando l'equazione che permette di determinare la distanza tra due punti nel piano, possiamo scrivere che:
Spostiamo un termine dal primo membro al secondo membro.
Eleviamo ora entrambi i membri al quadrato. Per ciò che riguarda il secondo membro, ricordiamoci che il quadrato di un binomio (o più in generale di due quantità che si sommano tra loro) è pari al quadrato della prima quantità, più il quadrato della seconda quantità, più il doppio prodotto della prima per la seconda.
Dopo aver sviluppato i quadrati, procediamo ad eliminare i termini uguali. Risulta infine:
Eleviamo nuovamente primo e secondo membro dell'equazione al quadrato:
Portiamo al primo membro tutti i termini con la x e la y. Al secondo membro tutti i termini noti:
Al primo membro metteremo in evidenza x², mentre al secondo a². Diviene:
Sostituiamo la quantità a²-c² con b², grazie all'equazione che abbiamo precedentemente illustrato introducendo l'asse minore dell'ellisse, e dividiamo entrambi i membri per a²b². Si ottiene infine:
Questa è l'equazione dell'ellisse, o meglio di un'ellisse con centro in corrispondenza dell'origine degli assi. Questo a patto naturalmente che le due quantità a e b non siano nulle.
Se a > b (come nel nostro caso) l'ellisse ha il semiasse maggiore disposto lungo l'asse x, mentre se a < b l'ellisse ha il semiasse maggiore disposto lungo l'asse y, e i suoi fuochi avranno coordinate: (0,c) e (0,-c). Varrà inoltre che:
Le ellissi sono figure geometriche caratterizzate da una certa "eccentricità" (ε). Precedentemente si è infatti parlato di come l'ellisse possa essere considerata la deformata del cerchio o della circonferenza. Ebbene, l'eccentricità di un'ellisse viene definita come il valore che esprime la deformazione dell'ellisse rispetto alla circonferenza. Più in dettaglio essa viene definita come il rapporto tra la semidistanza focale e il semiasse maggiore. Nel caso di ellisse con centro nell'origine degli assi ed asse maggiore orizzontale vale che:
Per qualunque ellisse ε < 1. Tanto maggiore è il valore dell'eccentricità, tanto più allungata è l'ellisse. Per ε = 0 l'ellisse degenera in un cerchio. Chiameremo invece le due rette di equazione
Qualora l'ellisse sia traslata, il suo centro non corrisponde più all'origine degli assi. Supponendo che esso abbia coordinate (xc, yc), l'equazione dell'ellisse diviene:
Le coordinate dei due fuochi vengono invece ad essere: (xc-c, 0) e (xc + c, 0).
E quelle dei quattro vertici: (xc + a, 0) e (xc -a, 0), (0, yc +b) e (0, yc - b).
