Proprietà  dell'ellisse

Proprietà dell'ellisse

Assi di simmetria, vertici e fuochi di un'ellisse

Nel corso di tutta questa scheda considereremo un'ellisse ? di equazione ( frac{x^2}{a^2} + frac{y^2}{b^2} = 1 ). Di volta in volta, a seconda che risulti ( a gt b ) o ( b gt a ), I fuochi di ? apparterranno all'asse ? o all'asse ?.

Osservazione 1: Consideriamo i punti ( A_1(-a, 0), A_2(a, 0), B_1(0, b), B_2(0, -b) ). Risulta subito evidente, operando una semplice sostituzione nell'equazione, che tutti e quattro i suddetti punti appartengono all'ellisse ?; si vede pure facilmente che essi sono le uniche intersezioni dell'ellisse con gli assi coordinati.

Definizione 1: Vertici di un'ellisse.

Si dice vertice di un'ellisse ciascuno dei quattro punti

, ovvero ciascuna delle intersezioni della curva ? con gli assi coordinati.

Osservazione 2: Supponiamo che il punto

appartenga ad ?. Allora è chiaro che anche i punti e appartengono ad ?, poiché

[ frac{x^2_P}{a^2} + frac{y^2_P}{b^2} = 1 Rightarrow frac{(pm x_P)^2)}{a^2} + frac{(pm y_P)^2}{b^2} = 1 ]

Questo dimostra che l'ellisse ?, indipendentemente dai valori assunti da ? e ?, risulta simmetrica rispetto agli assi coordinati. Ciò consente di dare la seguente definizione:

Definizione 2: Asse maggiore e asse minore

Si chiama asse maggiore di un'ellisse quello dei due segmenti

e sul quale giacciono i fuochi; è detto invece asse minore di un'ellisse l'altro dei due detti segmenti.

Osservazione 3: In base alla definizione 2, l'asse maggiore di un'ellisse con i fuochi disposti orizzontalmente è

, mentre quello minore è . Si noti che le lunghezze di detti segmenti sono rispettivamente e , e che per un'ellisse con i fuochi appartenenti all'asse delle ascisse vale . Dunque l'asse maggiore è effettivamente più lungo di quello minore, e ciò ne spiega i nomi.

Osservazione 4: Nel caso di un'ellisse con i fuochi appartenenti all'asse delle ordinate, vale un ragionamento del tutto simmetrico rispetto a quello fatto nell'osservazione 3. Dunque l'asse maggiore sarà quello verticale,

, mentre quello minore sarà .

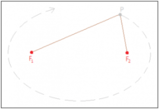
Osservazione 5: Consideriamo un'ellisse con i fuochi appartenenti all'asse delle ?, e in particolare facciamo riferimento all'immagine precedente. Il triangolo rettangolo

è tale che i cateti e siano lunghi rispettivamente ? e ?; poiché in quest'ellisse vale ( b = \sqrt{a^2-c^2} ), possiamo dedurre che . In un'ellisse orientata verticalmente, vale lo stesso risultato, ma naturalmente abbiamo che l'ipotenusa è lunga ?.

Osservazione 6: Le coordinate dei fuochi dipendono, come sappiamo, dal valore ?. Poiché è noto come questo si ricava a partire da ? e ?, che figurano nell'equazione di ?, possiamo dire senz'altro che

[ a gt b Rightarrow F_1( -\sqrt{a^2-b^2}, 0 ), ,,,, F_2(\sqrt{a^2-b^2}, 0) ]

Limitatezza ed eccentricità

Osservazione 7: Vogliamo dimostrare che il grafico dell'ellisse è tutto contenuto all'interno del rettangolo tratteggiato nella figura precedente, ovvero quello formato dalle parallele agli assi coordinati condotte per i vertici dell'ellisse. Ciò significherà che l'ellisse è limitata, ovvero che il suo grafico non si estende infinitamente nel piano come quello della parabola o della retta.

Prendiamo a questo proposito un qualsiasi punto

esterno al rettangolo; ciò implica che le coordinate di ? devono verificare almeno una delle due condizioni seguenti:

[ |x_P| gt a ,,, ext{ o } ,,, |y_P| gt b ]

Il punto ? non può appartenere all'ellisse. Infatti se così fosse dovrebbe risultare

[ frac{x^2_P}{a^2}+frac{y^2_P}{b^2} = 1 Rightarrow x^2_P = a^2Big( 1 - frac{y^2_P}{b^2} Big) ,,, \text{ e } ,,, y^2_P = b^2Big( 1 - frac{x^2_P}{a^2} Big) ]

ma se ( |x_P| gt a ), allora dalla seconda ( y^2_P ) dovrebbe essere negativo e ciò è assurdo; se poi fosse invece ( |y_P| gt b ), dalla prima ( x^2_P ) dovrebbe essere negativo è questo è ancora assurdo.

Ne deduciamo che un punto ? esterno al rettangolo non appartiene all'ellisse, e quindi che l'ellisse stessa è limitata.

Definizione 3: Eccentricità

Si definisce eccentricità ? di un'ellisse il rapporto tra la distanza focale e l'asse maggiore.

Osservazione 8: Nel caso di un'ellisse i cui fuochi appartengono all'asse delle ?, essendo l'asse maggiore lungo 2?, l'eccentricità si calcola come ?=?/?. Nell'altro caso risulta naturalmente ?=?/?. Poiché per entrambe le ellissi è sempre vero che la distanza focale è minore dell'asse maggiore, necessariamente sono verificate le disuguaglianze ( 0 le e le 1 ).

Osservazione 9: L'eccentricità è un parametro numerico che misura lo "schiacciamento" di un'ellisse, ovvero quanto essa differisce da una circonferenza. Nel caso limite ?=0, indipendentemente da quale sia l'ellisse di cui stiamo parlando, dovremo avere ?=0: ciò implica che i fuochi coincidono, e dunque che l'ellisse è in realtà una circonferenza.

Qualora invece dovesse risultare ?=1, allora l'asse maggiore sarebbe uguale alla distanza focale, ed essendo l'asse minore la radice della differenza dei loro quadrati, esso avrebbe lunghezza pari a 0: l'ellisse si riduce così ad un segmento, coincidente con l'asse maggiore.

Sia nel caso ?=0 che in quello ?=1 si suole dire che l'ellisse è degenere.

Altro materiale di supporto

Videolezione sull'ellisse