Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Nel caso di funzioni fratte, nella determinazione del dominio si deve tener conto degli eventuali punti in cui la funzione potrebbe non essere definita, e questi sono i punti per cui il denominat...

_stan
di _stan
5 min
Ominide
Vota
Appunto verificato
Contenuto originale e autentico, validato dal Team di Esperti di Skuola.net Informazioni appunto verificato Informazioni appunto verificato hover

Nel caso di funzioni fratte, nella determinazione del dominio si deve tener conto degli eventuali punti in cui la funzione potrebbe non essere definita, e questi sono i punti per cui il denominatore della funzione si annulla; in questo caso abbiamo:

[math] text(Denomina\tore) = 0 \to x + 1 = 0 \to x = - 1[/math]

Il dominio della funzione, quindi, è dato dall'insieme dei numeri reali eccetto in valore -1:

[math] D = R - {-1}[/math]

Determiniamo ora i punti di intersezione con gli assi:

[math] f(x) _|_ (x = 0) \to f(0) = 0 [/math]

Il punto individuato è quindi

[math] (0 ; 0) [/math]
.

[math] f(x) _|_ (y = 0) [/math]

[math] f(x) = 0 \to \frac{ \root[3]{x}}{x + 1} = 0 \to x = 0 [/math]

Il punto individuato è anche in questo caso

[math] (0 ; 0) [/math]
.

La funzione, quindi, passa per l'origine, e non ha altri punti di intersezione con gli assi.

Cerchiamo gli intervalli in cui la funzione è negativa e quelli in cui è positiva:

[math] f(x) > 0 \to \frac{ \root[3]{x}}{x + 1} > 0 [/math]

Studiando insegno si ottiene

[math] x > -1 vee x > 0[/math]
; la funzione in tale intervallo è positiva, mentre sarà negativa nell'intervallo
[math] -1 > x > 0[/math]
.

Studiamo la parità della funzione; ricordiamo che se

[math] f(-x) = f(x)[/math]
, la funzione è pari, ovvero simmetrica rispetto all'asse y, altrimenti se
[math] f(-x) = - f(x)[/math]
la funzione è dispari, ovvero simmetrica rispetto all'origine. In questo caso:

[math] f(-x) = \frac{ \root[3]{-x}}{-x + 1} = - \frac{ \root[3]{x}}{-x + 1} [/math]

uindi la funzione non è ne pari ne dispari.

Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso, a

[math]+oo[/math]
e
[math]-oo[/math]
:

[math] lim_(x \to oo) \frac{ \root[3]{-x}}{-x + 1} [/math]

Essendo il denominatore di grado maggiore den numeratore, tale limite vale 0, e questo valore si ha sia per

[math]+oo[/math]
che per
[math]-oo[/math]
. Abbiamo, quindi, la presenza di un asintoto orizzontale e, poiché il valore del limite è 0, l'equazione dell'asintoto orizzontale è
[math] y = 0[/math]
, ovvero l'asse x è asintoto orizzontale. Poiché la funzione non è definita in
[math] x = -1[/math]
, in tale punto potrebbe esserci un asintoto verticale; controlliamo quindi la sua eventuale presenza risolvendo i limiti destro e sinistro:

[math] lim_(x \to -1^+) \frac{ \root[3]{-x}}{-x + 1} , lim_(x \to -1^-) \frac{ \root[3]{-x}}{-x + 1} [/math]

Nel primo caso abbiamo:

[math] lim_(x \to -1^+) \frac{ \root[3]{-x}}{-x + 1} = \frac{-1}{0^+} = - oo [/math]

Mentre nel secondo caso:

[math] lim_(x \to -1^-) \frac{ \root[3]{-x}}{-x + 1} = \frac{-1}{0^-} = + oo [/math]

Quindi si ha un asintoto verticale sia destro che sinistro di equazione

[math] x = - 1[/math]
.

Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:

[math] f'(x) = frac( 1/3 x^{-2/3} (x + 1) - x^{1/3} )( (x + 1)^2 ) = [/math]

[math]frac( 1/3 x^{1/3} + 1/3x^{-2/3} - x^{1/3} )( (x + 1)^2 ) = [/math]

[math] frac( -2/3 x^{1/3} + 1/3 x^{-2/3} )( (x + 1)^2 ) [/math]

Troviamo i punti in cui la deriva prima si annulla:

[math] f'(x) = 0 \to frac( -2/3 x^{1/3} + 1/3 x^{-2/3} )( (x + 1)^2 ) = 0 [/math]

[math] 2/3 x^{1/3} = 1/3 x^{-2/3} \to frac(2x - 1)(x^{2/3}) = 0 \to x = 1/2 [/math]

Studiamo il segno della derivata prima:

[math] f'(x) > 0 \to frac( -2/3 x^{1/3} + 1/3 x^{-2/3} )( (x + 1)^2 ) > 0 \to [/math]

[math] frac( -2/3 x + 1/3 )( x^{2/3}(x + 1)^2 ) > 0 \to x > 1/2 [/math]

Dallo studio della derivata prima possiamo capire che la funzione sarà crescente per

[math]x>1/2[/math]
, quindi necessariamente essa presenterà un massimo (relativo) in
[math]1/2[/math]
; in particolare, in tale punto la funzione assume il valore:

[math] f(1/2) = \frac{1}{\root[3]{2}} \cdot \frac{1}{3/2} = \frac{ \root[3]{4}}{3} [/math]

Quindi, il punto

[math] ( \frac{1}{2} ; \frac{ \root[3]{4}}{3} ) [/math]
è un punto di massimo relativo per la funzione.

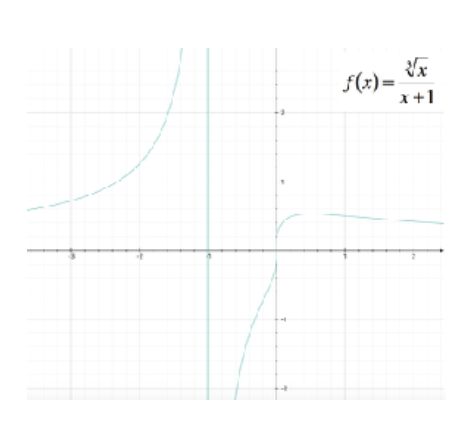
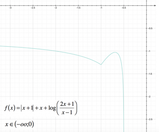
Possiamo quindi procedere rappresentando il grafico della funzione:

Potrebbe interessarti anche

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Vai al forum

I migliori insegnanti di Matematica

Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Matteo

Matteo S.

Supertutor
Verificato

Insegnante di Aiuto tesi, Algebra, Geometria, Matematica

a partire da 20 €/ora
most booked
Mostra altri Tutor