Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

Nel caso di funzioni logaritmiche, sappiamo che il dominio corrisponde all'insieme dei numeri reali per i quali l'argomento del logaritmo è positivo: x/4 > 0 to x > 0 Per cui: D = ( 0 ; +oo)...

_stan
di _stan
Ominide
3 min. di lettura
Vota

Nel caso di funzioni logaritmiche, sappiamo che il dominio corrisponde all'insieme dei numeri reali per i quali l'argomento del logaritmo è positivo:

[math] x/4 > 0 \to x > 0[/math]

Per cui:

[math] D = ( 0 ; +oo)[/math]

.

Determiniamo ora i punti di intersezione con l'asse x (con l'asse y non vi sono punti di intersezione, perché i punti per cui x = 0 sono esclusi dal dominio):

[math] f(x) _|_ (y = 0) [/math]

[math] f(x) = 0 \to x^2 [ \\log(x/4) - 1]^2 = 0 [/math]

[math]\\log(x/4) - 1 \to \\log(x/4) = 1 \to x/4 = e^1[/math]

[math] x/4 = e \to x = 4e [/math]

Il punto individuato è

[math] ( 4e ; 0 ) [/math]

.

Quindi la funzione ha un punto di intersezione con l'asse x.

Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a

[math]+oo[/math]

:

[math] lim_(x \to oo) x^2 [ \\log(x/4) - 1]^2 [/math]

Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:

[math] lim_(x \to oo) x^2 [ \\log(x/4) - 1]^2 = +oo [/math]

La funzione, quindi, non presenta asintoti orizzontali.

Cerchiamo la presenza di eventuali asintoti obliqui:

[math] m = lim_(x \to oo) frac(f(x))(x) = lim_(x \to oo) x [ \\log(x/4) - 1]^2 = +oo [/math]

Quindi non sono presenti neanche asintoti obliqui.
Studiamo ora il comportamento della funzione quando si avvicina al punto

[math](0;0)[/math]

(da destra):

[math] lim_(x \to 0^+) f(x) = lim_(x \to 0^+) [ frac(\\log(x/4) - 1)(x^{-1})]^2 = 0 [/math]

Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:

[math] f'(x) = 2x (\\log(x/4) - 1)^2 + x^2 (\\log(x/4) - 1) \cdot 4/x \cdot 1/4 = (\\log(x/4) - 1) (2x \\log(x/4) - 2x + 2x) =[/math]
[math] 2x \\log(x/4) (\\log(x/4) - 1)[/math]

Troviamo i punti in cui la deriva prima si annulla:

[math] f'(x) = 0 \to 2x \\log(x/4) (\\log(x/4) - 1) = 0 \to \\log(x/4) - 1 = 0 [/math]
[math] \\log(x/4) = 1 \to x/4 = e \to x = 4e [/math]

Studiamo il segno della derivata prima:

[math] f'(x) > 0 \to 2x \\log(x/4) (\\log(x/4) - 1) > 0 [/math]
[math] x > 0 [/math]
[math] \\log(x/4) > 0 \to x/4 > 1 \to x > 4 [/math]
[math] \\log(x/4) - 1 > 0 \to \\log(x/4) > 1 x/4 > e \to x > 4e [/math]

Dallo studio del segno si ottiene:

[math] ( 0 , 4 ) U ( 4e , +oo) [/math]

; la funzione, quindi, è crescente in tale intervallo; nell'intervallo

[math] ( 4 , 4e )[/math]

la funzione sarà decrescente.
Notiamo, quindi, che il punto

[math] ( 4e , 0 )[/math]

è un punto di minimo per la funzione.

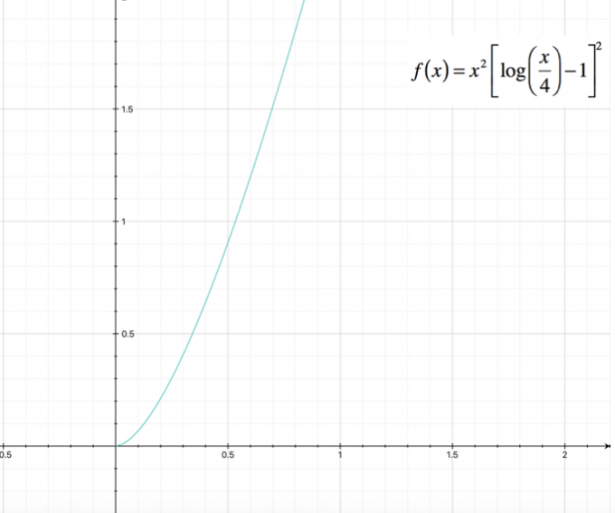
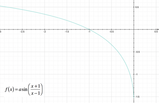
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:

Potrebbe interessarti anche

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Help (321322)
filo.22 di filo.22

Aiuto urgente per compiti
anitaminardi1987 di anitaminardi1987

Problema con potenze
gagix12 di gagix12

I migliori insegnanti di Matematica

Giovanni

Giovanni C.

Supertutor
Percorsi
Verificato

Insegnante di Aiuto tesi, Contabilità e bilancio, Controllo di gestione, Diritto

a partire da 20 €/ora
most booked
Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Mostra altri Tutor