Studio di funzione: Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. f(x) =

La funzione esponenziale di per se è definita in tutto R; in questo caso, però, l'esponente è una frazione, quindi, dobbiamo escludere dal dominio i valori che annullano il denominatore; in quest...

_stan
di _stan
Ominide
5 min. di lettura
Vota

La funzione esponenziale di per se è definita in tutto

[math]R[/math]

; in questo caso, però, l'esponente è una frazione, quindi, dobbiamo escludere dal dominio i valori che annullano il denominatore; in questo caso:

[math] 1 + x = 0 \to x = -1 [/math]

Quindi il dominio sarà l'insieme dei numeri reali eccetto il numero -1:

[math] D = R - {-1} [/math]

.

Determiniamo ora i punti di intersezione con gli assi:

[math] f(x) \in t x = 0[/math]

[math] f(0) = 0 \cdot e^{frac(0)(1 + 0)} =0 [/math]

Il punto individuato è

[math] ( 0 ; 0 ) [/math]

.

[math] f(x) _!_ (y = 0)[/math]

[math] f(x) = 0 \to x \cdot e^{frac(x)(1 + x)} = 0 \to x = 0[/math]

In entrambi i casi otteniamo come punto di intersezione l'origine degli assi.

Verifichiamo se la funzione è pari o dispari:

[math] f(-x) = - x \cdot e^{frac(-x)(1 - x)} [/math]

La funzione quindi non è ne pari ne dispari.

Cerchiamo gli intervalli in cui la funzione è positiva:

[math] f(x) > 0 \to x \cdot e^{frac(x)(1 + x)} > 0 \to x > 0 [/math]

Poiché l'esponenziale è sempre positiva, la funzione è positiva nell'intervallo:

[math] ( 0 ; +oo ) [/math]

.

Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a

[math]+oo[/math]

:

[math] lim_(x \to +oo) x \cdot e^{frac(x)(1 + x)} [/math]

Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:

[math] lim_(x \to +oo) x \cdot e^{frac(x)(1 + x)} = +oo [/math]

Analogamente, il limite a

[math]-oo[/math]

sarà:

[math] lim_(x \to -oo) x \cdot e^{frac(x)(1 + x)} = -oo [/math]

La funzione, quindi, non ha asintoti orizzontali; in questo caso possiamo passare alla ricerca degli asintoti obliqui:

[math] m = lim_(x \to oo) frac(f(x))(x) = lim_(x \to oo) e^{frac(x)(1 + x)} = e [/math]

Abbiamo trovato un valore finito del limite, che rappresenta il valore del coefficiente angolare dell'eventuale asintoto; proseguiamo con il calcolo dell'intercetta:

[math] q = lim_(x \to oo) [ f(x) - mx] = lim_(x \to oo) [ x \cdot e^{frac(x)(1 + x)} - ex] = [/math]

[math] lim_(x \to oo) [ x \cdot (e^{frac(x)(1 + x)} - e) ] = lim_(x \to oo) [ ex \cdot (e^{-frac(1)(1 + x)} - 1) ] [/math]

Cerchiamo di ricondurre il limite ad un limite notevole:

[math] lim_(x \to oo) [ frac(-ex)(x+1) \cdot frac((e^{-frac(1)(1 + x)} - 1))(-frac(1)(x+1)) ] = -e [/math]

Possiamo quindi determinare l'equazione dell'asintoto obliquo:

[math] y = ex - e [/math]

Poiché la funzione non è definita in

[math]x = -1[/math]

, verifichiamo se in tale punto è presente un asintoto verticale calcolando i seguenti limiti:

[math] lim_(x \to -1^+) x \cdot e^{frac(x)(1 + x)} , lim_(x \to -1^-) x \cdot e^{frac(x)(1 + x)} [/math]

I limiti destro e sinistro assumono i seguenti valori:

[math] lim_(x \to -1^+) x \cdot e^{frac(x)(1 + x)} = 0 [/math]

[math] lim_(x \to -1^-) x \cdot e^{frac(x)(1 + x)} = - oo [/math]

Quindi, la retta

[math] x = - 1[/math]

è asintoto verticale (sinistro) per la funzione; "da destra" la funzione si avvicina a tale punto, senza mai raggiungerlo.

Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:

[math] f'(x) = e^{frac(x)(1+x)} + x \cdot e^{frac(x)(1+x)} \cdot frac(1+x-x)((1+x)^2) =[/math]

[math] e^{frac(x)(1+x)} \cdot ( 1 + frac(x)((x+1)^2) ) = e^{frac(x)(1+x)} \cdot frac(x^2 + 3x + 1)((x+1)^2) [/math]

Troviamo i punti in cui la derivata prima si annulla:

[math] f'(x) = 0 \to e^{frac(x)(1+x)} \cdot frac(x^2 + 3x + 1)((x+1)^2) = 0 [/math]

[math] x^2 + 3x + 1 = 0 \to [/math]

[math] x = frac(-3 + \sqrt5){2} vee x = frac(-3 - \sqrt5){2} [/math]

Studiamo il segno della derivata prima:

[math] f'(x) > 0 \to e^{frac(x)(1+x)} \cdot frac(x^2 + 3x + 1)((x+1)^2) > 0 [/math]

[math] e^{frac(x)(1+x)} > 0 [/math]

[math] x^2 + 3x + 1 > 0 [/math]

[math] (x+1)^2 > 0 [/math]

Dallo studio del segno si ottengono i seguenti intervallo:

[math] ( - oo , frac(-3 - \sqrt5){2} ) uu ( frac(-3 + \sqrt5){2} ; +oo) [/math]

; la funzione, quindi, è crescente in tali intervalli.

Notiamo, quindi, che il punto individuato da

[math] x = frac(-3 + \sqrt5){2} [/math]

è un punto di minimo relativo per la funzione, mentre il punto individuato da

[math] x = frac(-3 - \sqrt5){2} [/math]

è un punto di massimo relativo per la funzione.

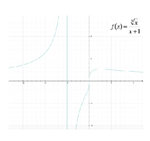
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:

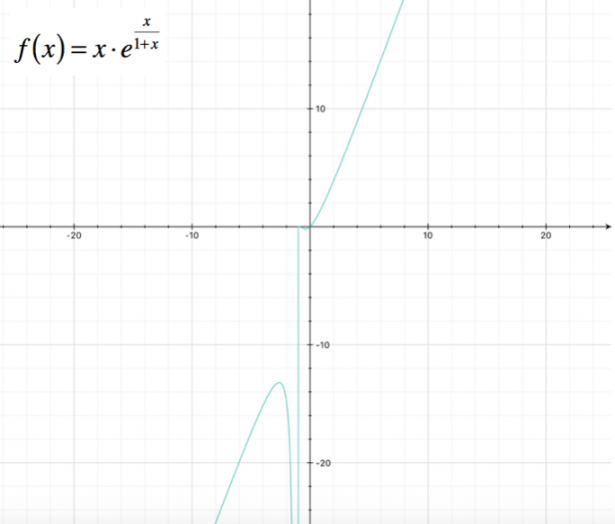
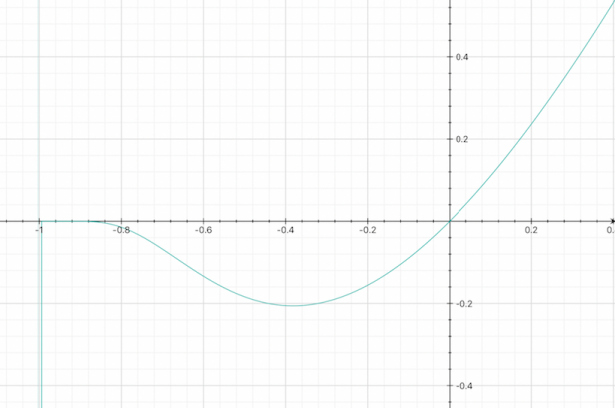
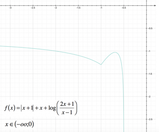
In dettaglio mostriamo l'andamento della funzione nell'intervallo

[math](-1 ; 0)[/math]

:

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Help (321322)
filo.22 di filo.22

Aiuto urgente per compiti
anitaminardi1987 di anitaminardi1987

Problema con potenze
gagix12 di gagix12

I migliori insegnanti di Matematica

Giovanni

Giovanni C.

Supertutor
Percorsi
Verificato

Insegnante di Aiuto tesi, Contabilità e bilancio, Controllo di gestione, Diritto

a partire da 20 €/ora
most booked
Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Mostra altri Tutor