Appunto di matematica per la scuola superiore che tratta del minimo comune multiplo e del massimo comune divisore. Come di consueto si propone un ripasso veloce degli argomenti necessari alla comprensione. Si parte con la scomposizione in fattori primi, le definizioni di multiplo e divisore di un numero naturale, con esempi svolti. Si prosegue con la definizione di minimo comune multiplo (m.c.m.) e di massimo comune divisore (M.C.D.). Le applicazioni numeriche conclusive completano la trattazione.
Indice
Scomposizione in fattori primi
I numeri naturali sono quelli dell’insieme indicato con N. Tra essi si definiscono numeri primi quelli che sono divisibili soltanto per uno e per se stessi. Ad esempio sono numeri primi 2,3, 5,7, 11, 13, 17, 19,….Non sono primi 4,12,25,30,…
Quando un numero non è primo è sempre possibile scomporlo in fattori primi, ovvero possiamo scriverlo sotto forma di un prodotto in cui tutti i fattori sono numeri primi.
Ad esempio il numero 30 si ottiene dal prodotto di 3 e 10, mentre il 3 è un fattore primo il numero 10 non lo è, infatti è dato dal prodotto di 2 per 5.
Il numero 30 scomposto in fattori primi è uguale a:
La scomposizione di un numero in fattori primi, in algebra, è detta fattorizzazione in numeri primi. Per effettuare la fattorizzazione, bisogna rivedere anche i criteri di divisibilità cioè i criteri che stabiliscono come capire se un numero è divisibile per alcuni fattori primi ricorrenti, come 2, 3, 5, 7, 11.
Multipli e divisori
Un numero naturale è multiplo di un altro se la divisione del primo per il secondo dà come resto 0. Attraverso la moltiplicazione possiamo trovare per ogni numero diverso da 0 infiniti multipli: basta moltiplicare il numero per 0, 1, 2, 3, 4, ... (il numero 0 ha invece come unico multiplo se stesso).Esempio
Scriviamo i primi multipli di 8:
ma ve ne sono infiniti altri, per indicarli sinteticamente possiamo scrivere:
Analogamente i multipli di 2 sono i numeri pari:
e per indicarli tutti usiamo la scrittura sintetica:
Un numero naturale diverso da 0 è divisore di un altro numero naturale se la divisione fra quest’ultimo e il numero dato è esatta, cioè se la divisione dà come resto 0.
Esempio
Il numero 6 è divisore di 18, perché
Mentre i multipli di un numero sono infiniti, i suoi divisori sono un numero finito.

Minimo comune multiplo
Il minimo comune multiplo di due o più numeri naturali, diversi da zero, è il più piccolo fra i multipli comuni. Il minimo comune multiplo e quindi un numero naturale intero. Il minimo comune multiplo di due o più numeri è il prodotto di tutti i fattori primi, comuni e non comuni, ognuno preso una sola volta, con l’esponente più grande. Se due numeri sono primi tra loro, il minimo comune multiplo è il loro prodotto. Vediamo un esempio, calcoliamo il minimo comune multiplo tra i numeri 8 e 9.Il numero 8, scomposto in fattori è uguale a
Il numero 9, scomposto in fattori è uguale a
I due numeri non hanno fattori in comune oltre l’unità, infatti ciascuno di essi è divisibile per uno e per se stesso e, i numeri sono primi tra loro e il minimo comune multiplo è il prodotto dei soli fattori non comuni ovvero
La procedura dunque è molto semplice:
- Si esegue la scomposizione in fattori dei numeri dati, che possono essere anche più di due
- Si individuano i fattori comuni e non comuni in tutti i numeri
- Si prendono tra i fattori individuati quelli con l’esponente massimo.
- Si effettua il prodotto dei fattori selezionati.
Massimo comune divisore, MCD
Il massimo comune divisore di due o più numeri naturali diversi da zero è il più grande fra i divisori comuni. Si ottiene come prodotto solo dei fattori primi che sono comuni ai numeri dati e, ciascuno va preso una sola volta con l’esponente più piccolo. Se il M.C.D. di due numeri è 1, significa che essi non hanno divisori comuni, tranne il numero 1.In questo caso i due numeri vengono detti primi tra loro.
Consideriamo la stessa coppia di numeri 8 e 9. abbiamo stabilito che sono primi tra loro, e il fattore comune è 1, quindi:
Saper calcolare il minimo comune multiplo e il massimo comune divisore, conoscendone bene la definizione è fondamentale nel calcolo letterale. Quando bisogna sommare le frazioni algebriche, si calcola il minimo comune multiplo dei denominatori. Quando si raccoglie a fattor comune tra due o più monomi, o come si suol dire “si mette in evidenza” si sta usando il massimo comune divisore. Attenzione a non confondere. Mai procedere in modo meccanico, bisogna capire cosa si sta facendo, solo così si evita di fare errori, a volte anche gravi.
Per ulteriori approfondimenti sul calcolo del MCD vedi anche qui
Esercizi svolti sul calcolo di mcm e MCD
Esercizio 1Calcolare m.c.m.(60,27)
Come detto prima scomponiamo in fattori primi i due numeri:
- il fattore comune ad entrambi è il 3, con il massimo esponente [math]\to 3^3[/math],
- i fattori non comuni sono: [math]\to 2^2 \\, 5[/math],
- moltiplichiamo i fattori come da definizione: [math]2^2 \cdot 3^3 \cdot 5[/math]
Esercizio 2
Calcolare M.C.D.(240,270)
Esercizio 3
Calcolare mcm tra 15, 45 e 75.
Partiamo come al solito dalla scomposizione dei vari numeri e poi terminiamo con il calcolo del mcm.

Problema 1.
Due amici sono nati nello stesso paese, ma si vedono raramente perché sempre in viaggio. Considerando che il primo torna a casa ogni 35 giorni mentre il secondo ogni 25 giorni, quando si incontreranno di nuovo nel paese dove sono nati?
Svolgimento
Ecco un esempio di problema che va risolto utilizzando il calcolo del minimo comune multiplo. Tipologia comune nei test di ammissione alle università. Andiamo allora calcolare il m.c.m. tra 25 e 35, per rispondere alla domanda posta nel problema. Scomponendo i due numeri in fattori si procede come segue:
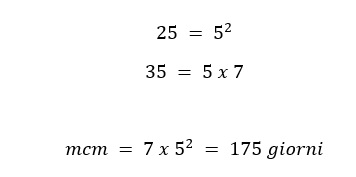








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo