Minimo comune multiplo: definizione ed applicazione

In questo appunto di Matematica viene spiegato il concetto di Minimo Comune Multiplo (mcm), ampiamente utilizzato in questa materia per la risoluzione di alcuni esercizi, soprattutto nel caso di equazioni frazionarie.

Minimo comune multiplo

In matematica, il minimo comune multiplo di due o più numeri interi positivi è il più piccolo numero intero positivo multiplo di ogni numero in questione; conseguentemente è anche il più piccolo numero divisibile per tali numeri.

Se consideriamo due numeri

, diremo che il minimo comune multiplo di a e b, e scriveremo

, è il più piccolo numero multiplo sia di a sia di b.
A questo punto è normale chiedersi: quando è utile calcolare il minimo comune multiplo?
Il minimo comune multiplo può essere utile per tante applicazioni, ma la più banale e nota è sicuramente quella relativa alle operazioni di somma e differenza tra due o più frazioni. Quando dobbiamo sommare due o più frazioni infatti, l’operazione di somma richiede come primo step quello di trasformare le frazioni date, in modo tale che tutte le frazioni coinvolte abbiano lo stesso denominatore; il denominatore comune utilizzato è proprio il minimo comune multiplo dei denominatori.
Nel caso particolare in cui uno tra a e/o b è uguale a zero, allora il {mcm}(a,b) è uguale a zero. È possibile calcolare il mcm di più numeri, sostituendo man mano due dei numeri con il loro comune multiplo e proseguendo fino a che non rimane un solo numero: il risultato; si può dimostrare che il risultato è lo stesso qualunque sia l'ordine in cui vengono fatte le sostituzioni. Ma vedremo meglio quali sono i passaggi da seguire nel prossimo paragrafo.

Calcolo del minimo comune multiplo: Esempi

Per capire come calcolare il minimo comune multiplo, passiamo all’applicazione pratica con un esempio.
Supponiamo di voler calcolare il minimo comune multiplo di due numeri interi e positivi:240 e 150. Il primo passaggio da fare è sicuramente la scomposizione in fattori primi di tali numeri. In questo caso avremo che la scomposizione di 240 è pari a:

• 240:2=120
• 120:2=60
• 60:2=30
• 30:2=15
• 15:5=3
• 3:3=1

Allora possiamo scrivere che:

Adesso ripetiamo lo stesso procedimento per il secondo numero:

• 150:2=75
• 75:5=15
• 15:5=3
• 3:3=1

Allora possiamo scrivere che la scomposizione di 150 è:

Nota la scomposizione dei numeri in questione, passiamo allo step successivo. In particolare, moltiplichiamo tra loro tutti i fattori primi comuni e non comuni, presi una sola volta con il più grande esponente.
Nel caso in esame abbiamo:

• 240: 2 con esponente 4, 5 con esponente 1 e 3 con esponente 1;
• 150: 2 con esponente 1, 5 con esponente 2 e 3 con esponente 1;

In questo caso tutti i fattori sono comuni, quindi prendiamo quelli con esponente maggiore, ovvero: 2 con esponente 4, 5 con esponente 2 e 3 con esponente 1. Moltiplicando tali fattori, otteniamo il minimo comune multiplo.
A questo punto possiamo dire che:

Per comprendere meglio quanto fatto, nel prossimo paragrafo sono riportati altri esempi.

Esercizi sul calcolo del mcm

: vogliamo calcolare il mcm(18,45). Per prima cosa, facciamo la scomposizione dei due numeri:

• 18:2=9
• 9:3=3
• 3:3=1

Allora possiamo scrivere che la scomposizione in fattori primi di 18 è:

Adesso ripetiamo lo stesso procedimento per il secondo numero:

• 45:5=9
• 9:3=3
• 3:3=1

Allora possiamo scrivere che la scomposizione di 45 è:

Adesso moltiplichiamo tra loro tutti i fattori primi comuni e non comuni, presi una sola volta con il più grande esponente. Nel caso in esame abbiamo: 2 con esponente 1, 3 con esponente 2 e 5 con esponente 1. Moltiplicando tali fattori, otteniamo il minimo comune multiplo:

Nell’immagine seguente è mostrato un’ulteriore esempio di calcolo del minimo comune multiplo.

Esercizio 2: Calcolare il mcm(60, 27).
Il primo passo è quello di scomporre ogni singolo numero in fattori primi e di trovare eventuali potenze. Vediamo subito come fare con 27 e 60.

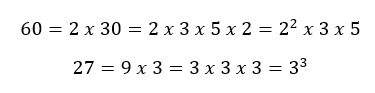
A questo punto prendiamo i diversi fattori trovati (2, 3 e 5) e possiamo calcolare il mcm:

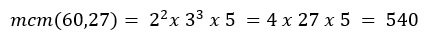
ESERCIZIO 3: Calcolare il mcm(240, 270).
Ancora una volta effettuiamo una scomposizione dei numeri di cui vogliamo calcolare il mcm.

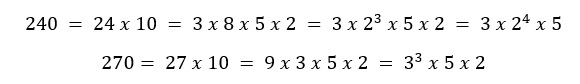
Da notare come nella scomposizione di 240 e 270 abbiamo utilizzato le proprietà delle potenze.

ESERCIZIO 4: Calcolare mcm tra 15, 45 e 75.
Partiamo come al solito dalla scomposizione dei vari numeri e poi terminiamo con il calcolo del mcm.

PROBLEMA 1: vediamo adesso una possibile applicazione.
Due amici sono nati nello stesso paese, ma si vedono raramente perché sempre in viaggio. Considerando che il primo torna a casa ogni 35 giorni mentre il secondo ogni 25 giorni, quando si incontreranno di nuovo nel paese dove sono nati?
Svolgimento: in questo caso viene richiesto il calcolo del mcm tra 25 e 35, perché i due amici si incontreranno nei multipli comuni di 35 e 25, e per la prima volta si incontreranno nel giorno che è il minimo dei multipli comuni. Per questa ragione possiamo scrivere:

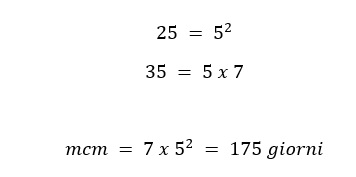
Oltre alle operazioni appena viste, è possibile calcolare il minimo comune multiplo di due o più numeri a partire dal loro Massimo Comun Divisore, come vedremo nel prossimo paragrafo.

Calcolo del mcm a partire dal MCD

Il minimo comune multiplo di due numeri a e b, diversi da zero, può essere calcolato anche a partire dal massimo comun divisore (MCD). In generale, tra il minimo comune multiplo e massimo comun divisore di due numeri interi positivi (a e b) vale la seguente relazione:

Utilizziamo gli stessi numeri del primo caso precedente per verificarne la validità, quindi scriviamo:

C.V.D.
Inoltre, per semplificare i passaggi matematici, ricordando che il MCD tra due numeri è multiplo di ciascuno di loro, si può iniziare l’operazione di determinazione del mcm dividendo uno dei numeri in questione per il massimo comun divisore e poi moltiplicare il risultato per il secondo numero.
Ad esempio, nel caso precedente avremmo potuto agire così:

• dividiamo uno dei due numeri per il MCD
  [math]\Rightarrow 240: 30=8[/math]
• moltiplichiamo il risultato per il secondo numero
  [math]\Rightarrow 8 \times 150= 1200[/math]

Abbiamo ottenuto nuovamente lo stesso risultato.
Ad ogni modo, un altro metodo per calcolare velocemente il minimo comune multiplo è utilizzando l'Algoritmo di Euclide, il cui appunto è presente tra i link di approfondimento del prossimo paragrafo.

Approfondimenti

In questo paragrafo sono riportati dei link di approfondimento utili alla comprensione di questo argomento:
Massimo comun divisore
Massimo comun divisore e Minimo Comune Multiplo
Operazioni tra frazioni
Numeri naturali
Algoritmo di Euclide