Concetti Chiave
- Una pallina di massa m ruota attorno a un asse verticale con velocità angolare ω costante, trattenuta da un filo inestensibile di lunghezza L.
- La relazione tra l'angolo θ e la velocità angolare ω è determinata tramite l'accelerazione centripeta e le forze in gioco.
- L'accelerazione centripeta è espressa come ac = ω²r, con r uguale alla distanza tra la palla e l'asse di rotazione.
- La tensione T è composta dalle forze mac e mg, che formano un triangolo rettangolo con T come ipotenusa.
- La formula finale ottenuta per ω in funzione di θ è ω(θ) = √(g/(Lcosθ)).
Una pallina di massa
[math]m[/math]
ruota attorno ad un asse verticale con velocità angolare [math]\omega[/math]
costante trattenuta da un filo inestensibile di lunghezza [math]L[/math]
. Sia [math]\theta[/math]
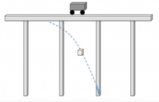
l'angolo evidenziato in figura. Trovare la relazione
[math]\omega(\theta)[/math]
che lega l'angolo [math]\theta[/math]
alla velocità angolare [math]\omega[/math]
.
Chiamiamo
[math]a_c[/math]
l'accelerazione centripeta. Uno dei tanti modi di esprimere l'accelerazione centripeta è questo [math]a_c=\omega^2r[/math]
(1). Nel nostro caso [math]r[/math]
è la distanza tra la palla e l'asse di rotazione.
La tensione
[math]T[/math]
si compone di due forze: [math]ma_c[/math]
e [math]mg[/math]
, ovvero i cateti del triangolo rettangolo avente [math]T[/math]
(i tre vettori formano un triangolo rettangolo). Per un noto teorema dei triangoli rettangoli, vale [math]ma_c=mg \cdot \tan \theta \implies a_c=g \cdot \tan \theta[/math]
(2)
Per un altro teorema riguardante i triangoli rettangoli, vale
[math]r=L \sin \theta[/math]
(3)
Sostituendo (3) e (2) nella (1) ottengo
[math]g \cdot \tan \theta=\omega^2L\sin \theta[/math]
da cui, sapendo che [math]\sin \theta/(\tan \theta)=\ cos \theta[/math]
e isolando [math]omega^2[/math]
a secondo membro ho, dopo due conti, [math]\omega(\theta)=\sqrt{g/(L\cos \theta)}[/math]
FINE
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
