Proporzioni - Calcolo del termine incognito

In questo appunto viene quindi spiegato il calcolo dell'incognita nelle proporzioni matematiche, attraverso delle espressioni matematiche.
Per comprendere bene tale appunto viene prima proposto un ripasso della definizione di proporzione e delle loro proprietà.
Al termine dell’appunto viene anche descritto il procedimento da seguire per risolvere una proporzione utilizzando la calcolatrice.

Le proporzioni

Una proporzione è un’uguaglianza tra due frazioni (ricordiamo che una frazione è una divisione tra due termini i quali vengono disposti sopra e sotto ad una linea di frazione).

Una proporzione viene quindi rappresentata nel seguente modo:
a : b = c : d

Dove a,b,c,d sono delle lettere che rappresentano dei numeri generici.

Le lettere prendono dei nomi particolari a seconda delle posizioni in cui si trovano:

• a,d prendono il nome di estremi (sono i termini che si trovano all’esterno della proporzione);
• b,c prendono il nome di medi (sono i termini che si trovano nelle posizioni intermendie della proporzione).

Proprietà delle proporzioni

Le proporzioni godono di alcune proprietà che sono molto utili per risolverle.
La prima proprietà delle proporzioni afferma che:
Il prodotto dei medi (b,c) è uguale al prodotto degli estremi (a,d).
Tale affermazione equivale a dire che:

La seconda proprietà di cui gode una proporzione afferma che:
Data una proporzione, se si scambiano gli estremi o i medi, o sia gli estremi che i medi, si ottiene una proporzione equivalente a quella di partenza.

Data la proporzione:
a : b = c : d
Tale affermazione equivale a dire che la proporzione considerata è equivalente alle seguenti proporzioni:
a : c = b : d (sono stati scambiati i medi)
d : b = c : a (sono stati scambiati gli estremi)
d : c = b : a (sono stati scambiati sia i medi che gli estremi)
Tali proprietà derivano dalle proprietà delle frazioni e dalle proprietà delle equazioni.
Per ulteriori approfondimenti sulle proporzioni e sulle loro proprietà vedi anche qua

Calcolo del termine incognito nelle proporzioni

Ecco come trovare il termine incognito (chiamato anche X) in una proporzione matematica di cui si conoscono i restanti termini. Per poter calcolare il termine incognito è possibile ricorrere alla proprietà fondamentale delle proporzioni secondo la quale il prodotto dei termini medi è uguale a quello degli estremi.

Prendiamo in esame la seguente proporzione e cerchiamo di trovare un modo per conoscere il valore del suo termine incognito aiutandoci con la proprietà fondamentale qui presentata:

Da cui si ricava:

Il risultato finale perciò è:

Verifichiamo:

Grazie a queste espressioni matematiche abbiamo ottenuto una proporzione, perciò possiamo affermare che in una proporzione il valore di un estremo incognito è uguale al prodotto dei medi diviso per l’altro estremo.

Il procedimento che viene utilizzato per calcolare il valore di un medio incognito è analogo. Per spiegarlo usiamo la seguente proporzione:

Applichiamo in questo caso la proprietà fondamentale:

Da cui si ottiene:

Il risultato finale che si ottiene quindi è:

Controlliamo bene:

Abbiamo ottenuto una proporzione: possiamo quindi enunciare la regola: in una proporzione il valore di un medio incognito è uguale al prodotto degli estremi diviso l’altro medio.

Non molto diverso risulta essere il procedimento per ottenere il calcolo del termine incognito di una proporzione continua. Consideriamo quindi la seguente proporzione continua:

Applichiamo quindi ora la proprietà fondamentale:

ovvero

da cui ricaviamo:

Il risultato finale che si ottiene è perciò

Accertiamoci di aver seguito il procedimento esatto:

Anche stavolta abbiamo ottenuto una proporzione: quindi si può affermare che in una proporzione continua il valore di un estremo incognito è uguale al medio proporzionale elevato al quadrato e diviso per l’altro estremo.

Adesso cerchiamo una regola che ci permetta di individuare il medio proporzionale di una proporzione continua. Consideriamo questa proporzione ed applichiamo la proprietà fondamentale:

Dato che l’operazione inversa dell’elevamento al quadrato è l’estrazione di radice quadrata otteniamo:

Quindi la proporzione è:

Verifichiamo:

e

Quindi possiamo affermare che in una proporzione continua il valore del medio proporzionale è uguale alla radice quadrata del prodotto degli estremi. Ecco spiegato il calcolo incognito nell'ambito delle proporzioni.

Per ulteriori approfondimenti sulla risoluzione delle equazioni di primo grado vedi anche qua

Calcolo del termine incognito nelle proporzioni con la calcolatrice scientifica

Collochiamoci nel menù:

C : Ratio

Passaggio #2

Iniziamo con il selezionare l’opzione 1.

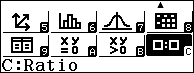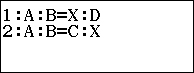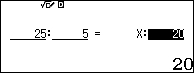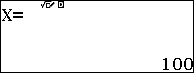
Inseriamo i valori

Passaggio #3

Digitando il tasto

Verrà visualizzato il valore cercato.

Qui di seguito il procedimento completo:

Ripetiamo la procedura per la seconda relazione

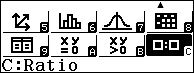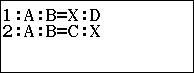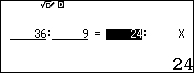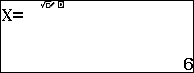
Passaggio #1

Collochiamoci nel menù:

C : Ratio

Passaggio #2

Iniziamo con il selezionare l’opzione 2.

Inseriamo i valori

Passaggio #3

Digitando il tasto

Verrà visualizzato il valore cercato

Qui di seguito il procedimento completo:

> > > Clicca qui e scopri tutte le funzioni della calcolatrice Casio FX-991EX!