Teorema di Pitagora - Formula e applicazione numerica

In questo appunto si parla del Teorema di Pitagora, un approccio schematizzato per gli alunni della scuola secondaria di primo grado, l’argomento è suddiviso in paragrafi per focalizzare l’attenzione sui principali elementi da tenere a mente: il triangolo rettangolo e i suoi elementi, l’equivalenza tra superfici piane, la formula del teorema e come ricavare le inverse. Completano l’appunto una semplice applicazione numerica per fissare le idee e alcune curiosità storiche.

Triangolo rettangolo - Elementi caratteristici

Il triangolo rettangolo è un triangolo che ha un angolo retto cioè un angolo di 90°, questo significa che due dei suoi lati sono sempre perpendicolari.

Le squadrette da disegno hanno la forma del triangolo rettangolo. I lati di questo tipo di triangolo hanno dei nomi particolari, il lato più lungo è detto ipotenusa gli altri due, quelli che formano l’angolo retto sono detti cateti. Per distinguerli vengono anche detti cateto maggiore e minore oppure cateto 1 e cateto 2. Gli altri due angoli del triangolo rettangolo sono sempre acuti ovvero minori di 90° e sono sempre complementari perché la loro somma da sempre 90°. Tornando all’esempio delle squadrette da disegno, in una ci sono angoli di 30° e di 60°, nell’altra sono uguali e misurano 45° ciascuno. Il triangolo rettangolo con i due angoli di 45° è detto anche isoscele; infatti, anche i suoi cateti sono uguali, inoltre questo tipo di triangolo è la metà di un quadrato e la sua ipotenusa coincide con la diagonale del quadrato stesso.

Teorema di Pitagora - Equivalenza tra superfici piane

Il teorema di Pitagora è valido esclusivamente per tutti i triangoli rettangoli, il suo enunciato stabilisce una equivalenza tra superfici piane. In geometria due superfici si dicono equivalenti se hanno la stessa estensione, ad esempio sono equivalenti due fogli A4 della stampante, oppure due banconote dello stesso taglio, come due da 5€. Due superfici equivalenti hanno la stessa area ma possono avere forma diversa. Facciamo un esempio: se per pavimentare due stanze di forma diversa, per una occorre un numero maggiore di piastrelle rispetto all’altra e abbiamo usato lo stesso tipo di piastrella, possiamo dire che la prima stanza ha un’estensione maggiore della seconda; se invece il numero di piastrelle utilizzate è lo stesso, concludiamo che le due stanze hanno la stessa estensione anche se la forma è diversa.
L’enunciato del teorema di Pitagora recita così: in ogni triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti

e

”. Se indichiamo rispettivamente con:

l’area del quadrato costruito sull’ipotenusa;

e

le aree dei quadrati costruiti sui due cateti;

vale la seguente equivalenza tra superfici:

Se calcoliamo l’area del quadrato che ha per lato l’ipotenusa, possiamo verificare che questa è uguale alla somma delle aree del quadrato che ha per lato il cateto

e del quadrato che ha per lato il cateto

.
Possiamo fare anche una verifica grafica del teorema usando un foglio quadrettato.

Formula del teorema di Pitagora

Ricaviamo ora dalla relazione in cui abbiamo eguagliato le aree dei quadrati, la relazione in cui ci sono le misure dei tre lati.
In un generico triangolo rettangolo siano rispettivamente:

la misura dell’ipotenusa

la misura del cateto maggiore

la misura del cateto minore

L’area di un quadrato è data dal prodotto lato per lato, quindi:

Ora riscriviamo la relazione tra queste aree:

Questa uguaglianza esprime il teorema di Pitagora in forma algebrica.

Formula inversa-ricavare i cateti

Dalla formula principale estraendo la radice quadrata si calcola la misura dell’ipotenusa:

La formula inversa consente di ricavare un cateto conoscendo l’ipotenusa e l’altro cateto.
Un cateto è uguale alla radice quadrata della differenza tra il quadrato dell’ipotenusa e l’altro cateto.
Riscriviamo la formula diretta:

Esplicitiamo ad esempio il cateto uno:

essendo elevato al quadrato, estraiamo la radice quadrata:

per ricavare il cateto due proseguiamo in maniera analoga, sotto radice avremo il cateto uno:

Applicazione numerica

Risolviamo un semplice problema con applicazione della formula inversa.
È dato un triangolo rettangolo di cui è nota la misura dell’ipotenusa e di un cateto, si chiede di calcolare la misura dell’altro cateto. Quando risolviamo un problema, per quanto semplice possa essere, cerchiamo sempre di adottare uno schema in cui avere sottomano i dati, le incognite e quindi i calcoli da fare.
Indichiamo con

e

le misure dei due cateti. Procediamo con lo svolgimento.
DATI:

Incognite:

Usiamo la formula inversa:

inseriamo i valori numerici:

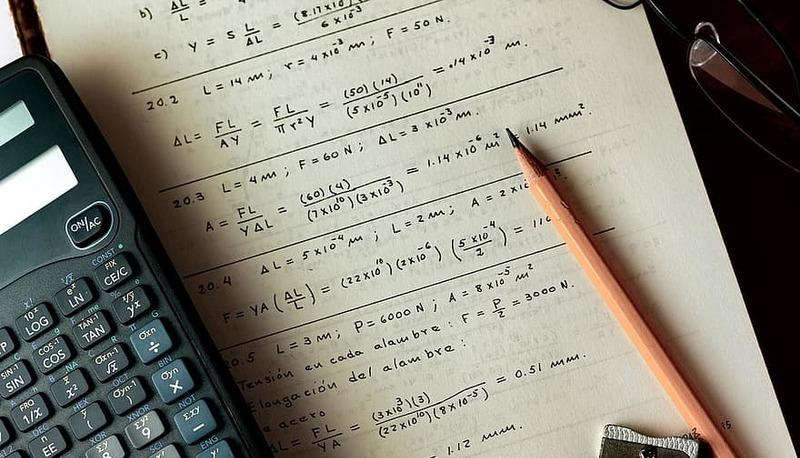
Teorema di Pitagora e terne pitagoriche

La relazione tra ipotenusa e cateti viene detta anche relazione pitagorica, utilizzandola è possibile stabilire se le misure dei lati di un triangolo qualunque si possano riferire a un triangolo rettangolo. Una terna pitagorica quando è formata da numeri primi fra loro, è detta primitiva. Le misure dei lati del triangolo rettangolo nel problema svolto sopra, costituiscono una terna pitagorica primitiva. I cateti e l’ipotenusa misurano rispettivamente 3,4,5. Verifichiamo la terna:

A partire da una terna primitiva si possono generare infinite terne pitagoriche, queste vengono dette terne derivate.

Curiosità sul teorema di Pitagora

Gli antichi egizi conoscevano la terna primitiva (3,4,5) e la utilizzavano per tracciare angoli retti precisi sul terreno. Adoperavano una corda richiusa agli estremi sulla quale vi erano 12 nodi posti a distanza di una unità l’uno dall’altro. La corda veniva tesa in tre punti particolari, potevano così formare un triangolo rettangolo con lati lunghi rispettivamente 3, 4 e 5 unità. L’angolo retta era situato tra il lato da 3 e quello da 4, perché il maggiore è l’ipotenusa.
Il teorema di Pitagora era noto già ai Babilonesi. Nella tavoletta Plimpton 322, che risale al 1800 a.C., è contenuta una tabella di alcune terne di lati di triangoli rettangoli, probabilmente utilizzati per calcoli astronomici. Al matematico Euclide si deve una formula generale per generare tutte le infinite terne pitagoriche.

Per ulteriori approfondimenti sul teorema di Pitagora vedi qua