Cos'è la geometria analitica: definizioni ed esempi

In quest'appunto è presente una definizione generale di geometria analitica, con una serie di esercizi svolti e commentati inerenti al calcolo della distanza tra punti e a figure geometriche come il rombo e i triangoli.

Cos'è la geometria analitica e cosa studia

La geometria analitica è una branca della matematica che si occupa dello studio dei principali enti geometrici attraverso l'ausilio di un piano cartesiano. In questo caso, quindi, i vertici delle figure sono dei punti aventi delle specifiche coordinate.

Una delle formule principali della geometria analitica riguarda il calcolo della distanza tra due punti. Esso può essere applicato sempre, purché si conoscano le coordinate dei due punti, in quanto per due punti passa una e una sola retta. Nei prossimi paragrafi vedremo delle applicazioni in ambito geometrico di questa formula.
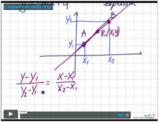
Esiste anche un'altra formula utilizzabile per il calcolo dell'equazione di una retta: essa richiede le coordinate di un punto e il coefficiente angolare della retta.

Esempio 1: Si dimostri che i punti di coordinate A(1,1),B(4,2),C(5,2) e D(5,4) possono essere i vertici di un rombo.

Come suggerito dalle principali nozioni di geometria piana, un rombo è un quadrilatero convesso avente tutti i lati di uguale lunghezza. Per risolvere l'esercizio occorrerà allora in primo luogo rappresentare i punti in un piano cartesiano, il quale aiuta a convincersi visivamente che il risultato del loro consecutivo congiungimento non sia un quadrilatero concavo. Successivamente dovremo calcolare le lunghezze dei lati e verificare che esse sono tutte uguali. A questo proposito usiamo la formula per il calcolo della distanza tra due punti:

Ne consegue che il quadrilatero risultante è effettivamente un rombo.

Esempio 2: Si dimostri che il triangolo ABC di vertici A(2,1),B(3,5) e C(6,2) è isoscele, quindi se ne determini l'area

Come nell'esempio 1, adoperiamo la formula della distanza tra due punti per calcolare le lunghezze dei tre lati del triangolo:

A quanto pare i lati

e hanno uguale lunghezza, e dunque il triangolo è isoscele di base . Per trovare l'area del triangolo possiamo adesso agire in due modi: o usiamo la formula di Erone, che consente il calcolo dell'area di un triangolo a partire dalle lunghezze dei tre lati, o cerchiamo di calcolare la lunghezza di una delle altezze. Il primo metodo è in questo caso piuttosto scomodo, in quanto le misure dei lati sono espresse attraverso dei radicali: troveremo quindi, detto il piede dell'altezza relativa a , la lunghezza di .

Dal momento che come abbiamo visto il triangolo è isoscele di base

, l'altezza e la mediana relative a questo lato coincidono; ciò implica che non è solamente il piede dell'altezza, ma anche il punto medio di . Possiamo quindi trovare usando la formula per le coordinate del punto medio di un segmento:

da cui possiamo avere che

Ricordando adesso che l'area di un triangolo si trova come la metà del prodotto della base e dell'altezza, avremo A =

.

Esempio 3: Si trovino il perimetro, l'area e il baricentro del triangolo

[math]ABC[/math]

i cui vertici sono A(3,1),B(1,3) e C(7,5).

Dopo aver rappresentato i punti in un piano cartesiano, passiamo a calcolare le lunghezze dei lati del triangolo con la formula della distanza tra due punti:

Potremo cos subito dire che il perimetro vale

Al contrario di quanto accadeva nel caso dell'esempio

, questa volta non sappiamo se il triangolo in esame è di qualche tipo particolare. Siamo dunque costretti a calcolarne l'area con l'ausilio della formula di Erone:

{Area} =

'

Per il baricentro adopereremo invece la formula che ci consente di calcolare le coordinate di

come media aritmetica di quelle dei vertici del triangolo:

G=( \frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3}) \Rightarrow G=(\frac{3+1+7}{3}, \frac{1+3+5}{3}) \Rightarrow G=( \frac{11}{3}, 3) )

Osservazione 1: Come già detto in tutti e tre gli esempi, il primo, fondamentale passo nella risoluzione di un esercizio di geometria analitica consiste nel rappresentare tutte le informazioni dateci dall'enunciato in un piano cartesiano. Questa operazione, se effettuata con accuratezza, consente spesso di trovare soluzioni altrimenti difficili da immaginare.

Osservazione 2: A dimostrazione di quanto detto nell'osservazione

, si consideri ancora l'esempio : se avessimo rappresentato opportunamente i tre vertici del triangolo, ci saremmo probabilmente accorti che esso è rettangolo. Ci avrebbe risparmiato il tedio di calcolarne l'area attraverso la formula di Erone.

Per ulteriori approfondimenti sulla geometria analitica, vedi anche qui